Antiderivative și nedeterminată integrală

§ 37. primitivă și nedeterminată integrală

În secțiunile anterioare am specificat funcția, ghidat de diferite formule și regulamente, găsiți derivatul său. Am văzut că derivatul are numeroase aplicații: derivat - o viteză de deplasare (sau, mai general, rata de apariție a oricărui proces); derivat - este panta tangentei la graficul funcției; utilizând funcția derivat poate fi investigată și monotonia extremelor; derivat ajută la rezolvarea problemelor pe optimizare.

Dar în viața reală, este necesar să se rezolve problemele inverse: de exemplu, împreună cu sarcina de a determina viteza de bine-cunoscut legea de mișcare întâlnite și problema restaurării legii de mișcare a ratei cunoscute. Luați în considerare una dintre aceste probleme.

Exemplul 1. Pe mai departe punctul de material în mișcare, viteza mișcării sale în timpul t este dat de u = tg. Găsiți legea de mișcare.

Decizie. Hai s = s (t) - legea dorită a mișcării. Este cunoscut faptul că e (t) = u „(t). Prin urmare, pentru a rezolva problema pe care trebuie să selectați o funcție s = s (t), din care derivatul este egal cu BAFF. Nu este greu de ghicit că

Imediat, observăm că exemplele de decizii corecte, dar incomplet. Am constatat că, de fapt, problema are infinit mai multe soluții: orice funcție de forma o constantă arbitrară poate fi legea de mișcare ca

Această sarcină a devenit mai sigur, a trebuit să se stabilească situația inițială: specificați coordonatele punctului în mișcare, în orice moment dat, de exemplu, la t = 0. Dacă, de exemplu, s (0) = s0. apoi din egalitatea obținem s (0) = 0 + C, t.e.S0 = S. Acum legea de mișcare este determinată în mod unic:
În matematică tranzacții reciproc inverse sunt atribuite diferite nume, veni cu o notație specială: de exemplu, disputându (x 2) și rădăcina pătrată, sinusoidală (sinh) și arc sine (arcsin x), etc. Procesul de a găsi un derivat al funcției predeterminate se numește diferențiere și funcționare inversă, adică proces de găsire a unei funcții pentru un anumit derivat - integrare.
Termenul „derivat“ poate fi justificată „într-un lumesc“: funcția y - f (x) „dă naștere la„o caracteristică nouă în = f“(x) • Funcția y = f (x) acționează ca un“ părinte „dar matematica desigur, nu o numesc“ părinte „sau“ producător“, se spune că este, în ceea ce privește funcția y«= f»(x), imaginea primară, sau, pe scurt, primitiv.

1. Determinarea funcției y = F (x) se numește primitivă pentru funcția y = f (x) la un interval predeterminat X, dacă pentru orice x din egalitatea X F „(x) = f (x).

În practică, diferența X nu este de obicei indicat, dar se înțelege (ca domeniu natural al funcției).

1) Funcția y = x 2 este un primitiv pentru functia y = 2x, deoarece pentru toți x avem (x 2) = 2x.
2) functia y - x 3 este funcția primitivă y Sx 2. deoarece pentru toate x, avem (x 3) = Sx 2.
3) Funcția y SINH este primitiv pentru functia y = sosh deoarece pentru toți x avem (sinh) = sosh.
4) Funcția yavlyaetya primitivă pentru funcția în intervalul, deoarece pentru orice x> 0 egalitatea
În general, cunoscând derivați cu formula pentru a găsi, vom crea cu ușurință un tabel cu formule pentru identificarea primitivelor.

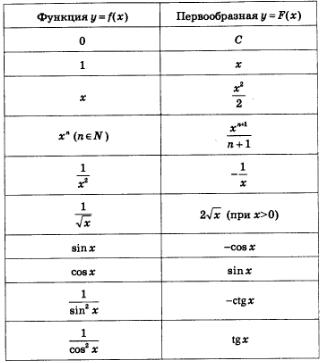
Sperăm că veți înțelege modul în care acest tabel se face: din care derivatul este înregistrat în a doua coloană este egală cu această funcție, care este înregistrată în rândul corespunzător al primei coloane (verifica, nu fi leneș, acest lucru este foarte util). De exemplu, pentru functia y = x 5 primitive instalați, este o funcție (vezi. Al patrulea rând al tabelului).

Note: 1. Aici vom demonstra o teorema că, dacă = F (x) - un primitiv pentru funcția y = f (x), atunci funcția y = f (x) este un număr infinit de primitive și toate dintre ele au forma = F (x) + C. prin urmare, ar fi mai bine în a doua coloană a tabelului adăuga pe tot termenul C, unde C - numărul real arbitrar.
2. concizie, uneori, în locul expresiei „functia y = F (x) este un primitiv pentru y funcție = f (x)», spune F (x) - primitivă f (x) ».

2. Normele pentru găsirea primitivele

În cazul în care caută Primitive ca atunci când găsirea derivații nu sunt numai cu formula (acestea sunt prezentate în tabelul de la pag. 196), dar unele reguli. Acestea sunt conectate direct cu instrumentele financiare derivate respective regulile de calcul.

Știm că derivata unei sume egale cu suma derivatelor. Această regulă dă naștere la o regulă corespunzătoare pentru identificarea primitivelor.

Regula 1. Primitivul din suma egală cu suma primitivelor.

Exemplul 2. Găsiți antiderivative a funcției y = 2x + cos x.

Decizie. Pentru primitiv 2 este x „; este un primitiv pentru cos x sin x. Deci, primitiv pentru funcția y = 2x + cos x va servi funcției y = x 2 + sin x (și, în general, orice funcție de forma y = x + 1 sinh + C).
Știm că putem lua factorul constant pentru semnul derivatului. Această regulă dă naștere la o regulă corespunzătoare pentru identificarea primitivelor.

Regula 2: Un factor constant poate fi luat în afara primitive.

Exemplul 3. Găsiți primitivele pentru o funcție dată:

. Fe w n un e) un primitiv pentru sin x x este -soz; Aceasta înseamnă, pentru funcția y = 5 sin x este o funcție y primitiv = x -5soz.

b) antiderivatives este cos x sin x; mijloace pentru funcția primitivă este o funcție de
c) un primitiv pentru x 3 este utilizat pentru primitiv este un primitiv pentru x y = 1 este funcția y = x. Folosind prima și a doua reguli pentru identificarea primitivelor, constatăm că primitiv pentru funcția y = 12x + 8x 3-1 este o funcție
Notă. După cum este bine cunoscut, produsul derivat nu este egal cu produsul derivatului (diferențiere a produsului, de obicei, mai dificil) și derivata privat nu este egal cu raportul dintre derivații. Prin urmare, nu există nici o regulă pentru a găsi produsul unui primitiv sau primitiv al raportului dintre două funcții. Fii atent!
Obținem o altă regulă pentru identificarea primitivelor. Știm că derivata funcției y = f (kx + m) se calculează cu formula:

Această regulă dă naștere la o regulă corespunzătoare pentru identificarea primitivelor.
Regula 3. Dacă = F (x) - primitiv pentru functia y = f (x), primitiv pentru funcția y = f (kx + m) este o funcție

Aceasta înseamnă că o funcție primitivă y = f (kx + m).
Semnificația a treia regulă este după cum urmează. Dacă știți că funcția primitivă y = f (x) este o funcție de y = F (x), a.vam nevoie pentru a găsi o funcție primitivă y = f (k, m +), apoi se procedează după cum urmează: să ia aceeași funcție ca și F, dar în loc de expresia argument x substitut kx + m; De asemenea, nu uitați să semneze funcția de înregistrare „factor de corecție“
Exemplul 4. Găsiți primitivele pentru o funcție dată:

Decizie. a) un primitiv pentru sin x x este -soz; Aceasta înseamnă, pentru funcția y = sin2h funcția primitivă va
b) antiderivatives este cos x sin x; mijloace pentru funcția primitivă este o funcție de

c) un primitiv pentru x 7 servește ca mijloc pentru funcția y = (4-5h) 7 este o funcție primitivă

3. nedefinită integrală

Am remarcat deja că problema găsirii unei primitive pentru funcția specificată la = f (x) are o soluție. Vom discuta această problemă în detaliu.

Dovada. 1. Fie y = F (x) - un primitiv pentru funcția y = f (x) pe X. interval Aceasta înseamnă că pentru orice x X, egalitatea x „(x) = f (x) Să ne găsim derivata oricărei funcții a formei. y = F (x) + C:
(F (x) + C) = F „(x) + C = f (x) 0 = f (x).

Astfel, (F (x) + C) = f (x). Aceasta înseamnă că = F (x) + C este un primitiv pentru funcția y = f (x).
Astfel, am demonstrat că, dacă funcția y = f (x) este un primitiv de la = F (x), atunci funcția 2. Noi acum dovedesc faptul că elementele specificate punctele de vedere epuizează setul de primitivelor.

Să = F1 (x) și y = F (x) - două primitivelor pentru funcția Y = f (x) pe X. interval Aceasta înseamnă că pentru toți x în intervalul X satisface relația: F ^ (x) = f ( x); F „(x) = f (x).

Funcția Rasmotrim y = F1 (x) -.F (x) și găsi derivatul său: (F, (x) F (x)) „= F [(x) F (x) = f (x) - f (x) = 0.
Este cunoscut faptul că, dacă derivata gap X este identic egal cu zero, atunci funcția este constantă în intervalul X (vezi. Teorema 3 § 35). Prin urmare, F1 (x) F (x) = C, de ex Qx) = F (x) + C.

Exemplul 5 dat legea modificărilor vitezei din timp v = -5sin2t. Găsiți mișcarea de s = s (t), în cazul în care se știe că la momentul t = 0 punct coordonatei este egal cu numărul de 1,5 (adică s (t) = 1,5).

Decizie. Deoarece rata - coordonatele derivată în funcție de timp, trebuie să găsim mai întâi un primitiv de viteza, adică primitiv pentru funcția v = -5sin2t. O astfel de caracteristică este primitivele. un set de primitivelor este după cum urmează:

Pentru a găsi o anumită valoare a constantei C, folosim condițiile inițiale potrivit cărora s (0) = 1,5. Substituind formula (1), valorile t = 0, S = 1,5, obținem:

Substituind valoarea C în formula (1), vom găsi suntem interesați în legea de mișcare:

DEFINIȚIE 2. Dacă funcția y = f (x) este cuprins în intervalul X primitiv = F (x), mulțimea primitivelor, adică o multitudine de funcții de forma y = F (x) + C, numită integrală nedefinită a funcției y = f (x) și reprezintă:

(Read: "integrala nedefinită a X EFF de X").
În secțiunea următoare vom afla ce sensul ascuns al acestei denumiri.
Pe baza tabelului existent în această secțiune primitivii alcătuiesc un tabel de integralelor nedefinite de bază:

Pe baza celor de mai sus trei reguli pentru găsirea primitivii putem formula regulile relevante de integrare.

Articolul 1. Integrala suma funcțiilor este egală cu suma integralelor acestor funcții:

Regula 2: Un factor constant poate fi luată în afara semnului integrală:

Exemplul 6. Găsiți integralele nedefinite:

Decizie. a) Folosind prima și a doua reguli de integrare, obținem:

Acum folosim 3 si 4 formule de integrare:

Ca rezultat, obținem:

b) Folosind a treia regula de integrare și Formula 8, obținem:

c) găsirea unui ordin predeterminat direct integral nu avem nici o formulă corespunzătoare sau regula corespunzătoare. În astfel de cazuri, uneori ajuta la expresii de conversie identice preformați conținute în integrandul.

Noi folosim formula trigonometrice coborâre de studii:

Apoi ne-am găsit succesiv:

AG Mordkovich Algebra Grad 10

Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.

Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.