Bazele rezistenței materialelor

Anterior, pentru simplitate și claritate, este de obicei privit ca un grinzi riglă de lemn care a permis cunoscute ipoteze pentru a obține ecuațiile de bază și formulele de calcul al capacității purtătoare a fasciculului. Cu aceste ecuații am construit diagrame ale forțelor laterale „Q“ și îndoire momentul „M“.

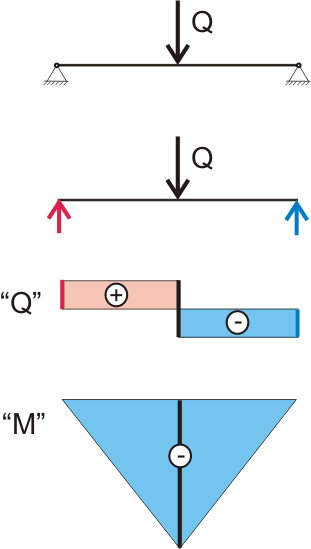
Figura 149.2.1. Diagrame de forțe transversale și momente de încovoiere care acționează în secțiunile transversale ale fasciculului la sarcină punct.

Ceea ce în cele din urmă a permis simplu și clar determina valoarea momentului maxim de încovoiere și deci valoarea tracțiune normală maximă și tensiuni de compresiune în cea mai încărcată secțiune transversală a fasciculului.

Apoi, cunoscând rezistența calculată a materialului fasciculului (valori calculate sârmă rezistență conform SNIP) poate determina foarte ușor modulul secțiunii, iar apoi alți parametri ai fasciculului, înălțimea și lățimea, dacă o grindă de secțiune transversală dreptunghiulară, diametrul, în cazul în care secțiunea circulară număr grindă sortiment de, în cazul în care un fascicul de un profil metalic laminate la cald.

Un astfel de calcul este un calcul al puterii pe primul grup de state care limitează și pentru a determina sarcina maximă care poate rezista la construcție calculată. Depășirea sarcina maximă admisă va duce la eșec structurale. Cum se va rupe în jos de proiectare, avem în acest caz, nu este interesat, deoarece acest site nu este vorba despre probleme de studii teoretice și practice ale statelor limită de materiale, ci numai unele dintre metodele de calcul ale structurilor cele mai comune de construcție.

inginerie de proiectare, în mod obișnuit calculele care vor fi folosite de sute de tone și zeci de metri cubi efectuate, astfel încât să se obțină designul maxim încărcat. Prin urmare, astfel de calcule sunt factori complexe și variate, luând în considerare durata de viață a structurii, natura sarcinilor, sarcini ciclice, dinamice, eterogenitatea materialului utilizat, etc. - zeci. Acest lucru este logic, deoarece producția brută de fiecare procent, ca urmare prevede economii tangibile. Într-o anumită construcție, se execută o dată, rezistența structurală, chiar și cu o marjă dublă este mai importantă decât posibilele economii de materiale și, deoarece calculele pentru construirea privat mic de inaltime poate fi la fel de simplu posibil, folosind factorul doar o corecție γ = 1,6 ÷ 2 în cazul în care acest factor va fi multiplicat valorile tensiunii sau γ = 0,5 ÷ 0,7, în cazul în care acest raport este înmulțită cu valoarea rezistenței calculată. Cu toate acestea, acest lucru chiar astfel de calcule simple nu sunt limitate.

Orice fascicul având o lungime substanțial mai mare decât înălțimea secțiunii transversale, care este o tijă sub sarcină se va deforma. Rezultatele sunt deplasarea de deformare a axei centrale a fasciculului în raport cu y -axis. pune pur și simplu deformarea și rotirea fasciculului secțiune transversală în raport cu planul secțiunii transversale. Și cele mai multe dintre aceste deturnări și unghiurile de rotație, indiferent de ce fel de sprijin din grinzi și orice sarcină care acționează pe ea poate fi, de asemenea, determinată. Diagrama corespunzătoare pentru determinarea unei secțiuni transversale deplasate ca urmare a devierii cel mai mult și care este înclinată mai sunt de asemenea construite pentru a determina unghiul maxim de cotitură și deformarea maximă.

Figura 174.5.6. Diagrama unghiurilor de rotație prin acțiunea sarcinii concentrate în mijlocul grinzii

Diagrama Deformare nu este dat aici, dar destul de ciudat, este diagrama cea mai simplă care arată poziția axei care trece prin secțiunea transversală a fasciculului, ca urmare a deformării și Epure personal poate fi văzut pe orice fascicul suficient de secuiasca sau orice alt model. Cunoașterea modulului de material și momentul de inerție al fasciculului aria secțiunii transversale pentru a determina deformarea maximă este, de asemenea, nu este foarte dificil. Simplificați aceste sarcini permit modele de proiectare pentru grinzi. care în funcție de natura și de tipul de încărcare suportă formulele corespunzătoare sunt date.

Aici cititorul poate fi o întrebare rezonabilă, și ceea ce a fost nevoie pentru a construi epure forfecare subliniază „Q“, în cazul în care, în orice calcul a acestei diagrame nu este implicat. Ei bine, e timpul să răspundă la această întrebare.

Faptul că calculul diferitelor tipuri de grinzi, secțiune transversală dreptunghiulară, în special constantă situată orizontal, rezistența prin acțiunea tensiunilor tangențiale este foarte rar determina, spre deosebire de calculele de mai sus. Cu toate acestea, știu ce - stresul de forfecare - și modul în care acestea afectează proiectarea lucrărilor, chiar dacă este foarte simplist, dar încă mai este necesar.

Astfel cum rezultă din definiția, tensiunile de forfecare care acționează în planul secțiunii transversale, așa cum s-ar referi la secțiunea transversală și sunt numite pentru că tangente. Se determină valoarea tensiunilor de forfecare la prima vedere, pur și simplu împărți valoarea forței laterale (pentru că avem nevoie pentru schema de „Q“), aria secțiunii transversale (în exemplul nostru, forțele laterale care acționează numai de-a lungul axei y și dincolo de aceasta, ne-ar fi de ajuns pentru a complica orice calcul, vom avea întotdeauna timp):

Ca rezultat, putem construi stres tangențială epure „τ“ (în plus față de stresul normal „σ“) din formularul de mai jos:

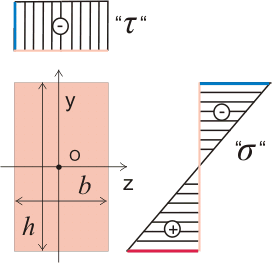
Figura 270,1. Diagrama preliminară a tangențială de stres „τ“

Cu toate acestea, o astfel de stres tangențiale curba ar fi valabil pentru un material abstract având elasticitate liniară de-a lungul axei y. și un rigid de-a lungul axei z. prin care în secțiune transversală a unui astfel de material nu există o redistribuire a tensiunilor și există doar un singur tip de deformare în raport cu axa y. De fapt, orice organism având proprietăți izotrope, sub influența stresului încearcă să mențină volumul său, și, prin urmare, avem în vedere secțiunea transversală încearcă să păstreze zona lor. Un exemplu ilustrativ este atunci când stai pe minge, înălțimea ei sub influența greutatea este redusă, dar lățimea este crescută. Mai mult decât atât, acest proces nu este liniar. Dacă tăiați cubul aluat sau paralelipiped, apoi apăsați pe el, acesta va deveni convexe fețele laterale, un proces similar are loc in testele de laborator pe metal de compresie specimene sau alte materiale.

În plus, aceasta înseamnă, de asemenea, că tensiunile de forfecare care acționează de-a lungul axei y. provoca apariția tensiunilor de forfecare de-a lungul axei z și tensiunile de forfecare diagrama de-a lungul axei z va fi mai clar arată tensiunile tangențiale schimbă în raport cu înălțimea fasciculului. Forma diagramei va semăna cu o față laterală a unui cub aplatizată a testului, iar zona a diagramelor desigur, nu se va schimba. Ie Valori diagrama tensiunilor tangențiale la partea de jos și la partea de sus a secțiunii transversale va fi zero și valoarea maximă (pentru o secțiune transversală dreptunghiulară) va fi înălțimea secțiunii de mijloc și în mod clar mai mult Q / F. Bazat pe condiția ca valoarea maximă a zonelor de diagrame diagrame de forfecare nu poate fi mai mare de 2Q / F, și apoi numai în cazul în care diagrama va fi de două triunghiuri, în acest caz, valoarea maximă este înălțimea triunghiului. Cu toate acestea, așa cum am văzut diagrama unui tip mai mult ca o parte dintr-un cerc sau a unei parabole, adică, Valoarea de stres maxim de forfecare ar fi de aproximativ 1.5Q / F:

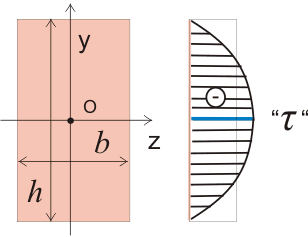
Figura 270.2. O diagramă mai precisă a tensiunilor tangențiale.

Rând gri prezintă diagrama adoptate anterior tensiunile de forfecare de contact, dar acum tensiunile de forfecare direcționată de-a lungul axei z.

Matematic, schimbare de forfecare în funcție de înălțimea secțiunii poate fi exprimată în termenii schimbării momentului static al secțiunii tăiate, reglarea lățimii secțiunii, deoarece fasciculul nu au întotdeauna o formă dreptunghiulară în secțiune transversală. Ca rezultat, o formulă pentru determinarea tensiunilor de forfecare (derivare nu este prezentată aici) are următoarea formă:

în care Qy - valoarea forței laterale în secțiune transversală considerată a diagramei definită prin „Q“

Sz UTS - un moment static al unei secțiuni tăiate a altitudinii în cauză în raport cu axa z. Definită ca aria porțiunii tăiată, înmulțită cu distanța dintre centrul de greutate al centrului secțiunii transversale de greutate și partea retezată a secțiunii. De exemplu, în partea de jos a secțiunii transversale, adică, la înălțimea h = 0, aria secțiunii porțiunea tăiată va fi, de asemenea, egal cu 0, și, prin urmare, tensiunile de forfecare care acționează asupra secțiunii transversale lățime b, după cum va fi zero. Pentru secțiunea transversală care trece prin centrul de greutate al secțiunii transversale, adică, la înălțimea porțiunii secționat a secțiunii transversale egală cu h / 2, va fi un cuplu static (bh / 2) (h / 4) = bh 2/8. În cazul în care înălțimea secțiunii tăiate egală cu înălțimea secțiunii transversale a momentului static va fi zero, deoarece centrul de greutate al părții secționat a secțiunii, în acest caz, ar coincide cu centrul de greutate al secțiunii transversale.

b - lățimea secțiunii transversale a înălțimii secțiunii transversale observate. Pentru grinzi cu secțiune constantă Lățimea secțiunii dreptunghiulare, dar sunt grinzi rotunde, T-bar, I formă sau orice altă secțiune. Mai mult decât atât, definiția mai forfecare accentuează numai, și este utilizat în calculul grinzii nu este dreptunghiular, la fel ca în secțiunea de tranziție a rafturilor în perete există un salt semnificativ de forfecare datorită modificărilor lățimii secțiunii transversale, trecerea de la flanșa în peretele are loc, în general, la o astfel de înălțime în cazul în care tensiunile normale sunt suficient de mari, și ia în considerare calculele relevante.

Iz - momentul de inerție al secțiunii transversale în raport cu axa z. În acest caz, doar mai puțin constantă. Pentru un moment, secțiune transversală dreptunghiulară a inerției este bh 3/12.

Astfel, conform formulei (270,2), tensiunea maximă tangențiale va fi:

Același rezultat ne și geometria a dat.

Și altul. Pentru materiale cu proprietăți anizotrope pronunțate, de exemplu, pentru rezistența la inspecția lemnului de forfecare necesare. Faptul că puterea lemnului de-a lungul cerealelor și compresiune rezistența lemnului la compresiune perpendicular pe cereale - sunt lucruri complet diferite. Prin urmare, verificarea este efectuată la secțiuni transversale în care tensiunile de forfecare sunt maxime, de obicei, o secțiune transversală grindă pe suporturile (sarcina dacă uniform distribuite). În acest caz, tensiunile de forfecare care rezultă o valoare este comparată cu valoarea calculată a rezistenței la compresiune sau prăbușirea lemnului peste cereale - Rc90.

Cu toate acestea, există o altă abordare pentru a determina tensiunile de forfecare: sub grindă sarcină este deformată, normale maxime de compresiune și întindere tensiunile apar în partea de jos și în secțiunea transversală superioară a grinzii, care poate fi văzută din diagrama „sigma“ la ris.270.1 .

În acest caz, fibrele materialului neomogene, cum ar fi lemnul, și într-adevăr, între straturi de orice alt material având tensiunile de forfecare, este acum îndreptată de-a lungul axei x. și anume pe aceeași axă ca și tensiunile de compresiune normale și tangențiale care apar ca rezultat al momentului de încovoiere.

Acest lucru se întâmplă prin faptul că fiecare experiență strat considerat semnificativ diferite de sarcină normală și, ca urmare toate aceeași redistribuire a tensiunilor și eforturi de forfecare apar. Aceste tensiuni de forfecare ca și în cazul în care încercarea de a împărți fasciculul în straturi separate, fiecare dintre care va funcționa ca un fascicul separat.

Diferența de rulment capacitate între straturi individuale și întregul fascicul este clar. De exemplu, dacă luăm un teanc de foi de hârtie, chiar și în 500, apoi îndoiți un astfel de pachet - o bucată de tort, și dacă toate colile să se lipească între ele, și anume straturi grinzi împreună, vom obține întregul fascicul și aici trebuie să fie mult mai dificil să se aplece. Dar, între foile lipite împreună, și va apărea foarte aceeași, relativ vorbind, tensiunile normale de forfecare. Cu toate acestea, valoarea normală este determinată de tensiunile de forfecare în același mod și în calculele implicate este aceeași forță de forfecare este determinată de diagrama „Q“. Asta nu doar considerat tăiat și forfecare a secțiunii transversale, respectiv, momentul static poate fi indicată - Sz ck. În acest caz, tensiunile de forfecare care rezultă o valoare este comparată cu valoarea calculată scindarea rezistenței lemnului lungul cereale - Rck.

Adevărat, valoarea RS90 si lemn Rck au același sens, dar subliniază totuși tangențiale de acțiunea forțelor de forfecare și a deformărilor provocate de îndoire pentru a distinge (întrucât considerăm că două perrpendikulyarnye reciproc zona de stres principal), și direcția de acțiune a tensiunilor de forfecare este importantă în determinarea tensiunii totale la punctul de sub corpul.

Cu toate acestea, toate acestea nu este nimic mai mult decât comună concepția de eforturi de forfecare. În materialele reale prin procesul de redistribuire stres mult mai complicat, toate pentru că chiar și din metal atribuită materialelor izotrope poate fi destul de arbitrar. Cu toate acestea, aceste aspecte sunt considerate discipline științifice separate - teoria elasticității. La calculul construcțiilor care constituie tije - grinzi sau plăci - plăci pe dimensiunea camerei, este posibil să se utilizeze formula (270.2), derivată pe baza pozițiilor comune ale teoriei elasticității liniare. La calcularea organismelor masive ar trebui să utilizeze metodele de elasticitate neliniare.

Numărul de terminal Yandex Wallet 410012390761783

Sau pe harta 5106 2110 0462 8702 Destinatar Sergei Gutov

Ucraina - grivna numărul de card (Privatbank) 5168 7423 0569 0962 Destinatar Gutov Serghei Mihailovici

În orice caz, o pungă WebMoney: R158114101090