Ca traduce fracție zecimală într-o metodă obișnuită de 3

Aici, s-ar părea, zecimal convertit în utilizãrile - tema elementară, dar mulți studenți nu-l înțeleg! Așa că astăzi, vom discuta mai multe algoritmi, cu care se va înțelege cu orice fracții în doar o secundă.

Permiteți-mi să vă reamintesc că există cel puțin două forme de înregistrare aceeași împușcat: ordinare și zecimale. Zecimale - aceasta este tot felul de tip proiectare 0,75; 1,33; și chiar -7.41. Dar exemple de fracțiuni, care exprimă aceleași numere:

Acum vom înțelege modul în care intrările zecimale merge la obicei? Și cel mai important, cum să facă acest lucru cât mai repede posibil?

Algoritmul de bază

De fapt, există cel puțin doi algoritmi. Și acum ne vom uita la ambele. Să începem cu primul - cel mai simplu și ușor de înțeles.

Pentru a converti o zecimală la un vulgar, trebuie să efectuați trei pași:

1. Rescrie împușcat inițial ca o nouă fracție: numărătorul va rămâne zecimal original și numitorul este necesară pentru a pune unitatea. Semnul numărului inițial este, de asemenea, plasat în numărător. De exemplu:

Inmultiti numărătorul și numitorul fracției obținute la 10 până virgulă dispare în numărătorul. Amintește la fiecare multiplicare prin virgulă de 10 este deplasat dreapta cu un caracter. Desigur, deoarece numitorul este multiplicată, de asemenea, în cazul în care în loc de numărul 1 va apărea 10, 100, etc. exemple:

Algoritmul procedeaza la fracțiile uzuale

În final, reducerea fracției rezultată a modelului standard de: diviza numărătorul și numitorul prin numărul celor cărora le sunt multipli. De exemplu, în primul exemplu, 0,75 = 75/100, și ambele 75 și 100 sunt împărțite de 25. Deci, vom obține $ 0,75 = \ frac = \ frac = \ frac $ - asta e tot răspunsul :).

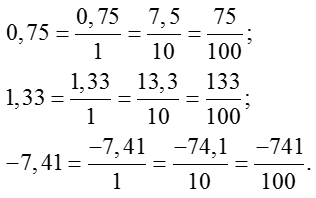
Notă importantă despre numere negative. Dacă exemplul inițial cu fracția zecimală este un semn „minus“, și apoi de ieșire la fracțiunea comună trebuie să fie, de asemenea, „negativ“. Iată câteva exemple:

Exemple de tranziție de la fracții zecimale convenționale

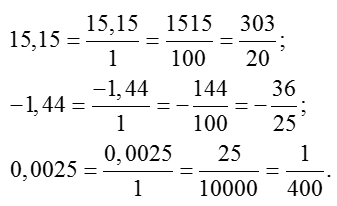
O atenție deosebită trebuie acordată ultimul exemplu. După cum vom vedea, există multe 0,0025 fracțiune de zerouri după virgulă. Din acest motiv avem deja cât mai multe de patru ori pentru a se multiplica numărătorul și numitorul de 10. Pot cumva simplifica algoritmul în acest caz?

Desigur, poți. Și acum ne uităm la un algoritm alternativ - este un pic mai greu de înțeles, dar după un pic de practică ruleaza mult mai rapid decât standardul.

mod mai rapid

Algoritmul de asemenea, 3 pași. Pentru a obține o fracțiune zecimal obișnuit, procedați în felul următor:

1. Calculați cât de multe cifre după virgulă este în valoare. De exemplu, fracțiunea 1,75 din cele două numere, iar la 0,0025 - patru. Notăm acest număr de litera $ n $.
2. Rescrie numărul inițial ca o fracțiune de forma $ \ frac ^ >> $, în cazul în care $ a $ - este toate cifrele din fracțiunea inițială (fără „start“ pe zerouri la stânga, dacă este cazul), și $ n $ - este numărul de cifre după virgulă, am considerat primul pas. Cu alte cuvinte, este necesar să se împartă cifrele inițiale ale fracțiunii pe unitate la $ n $ zerouri.
3. Dacă este posibil, se reduce fracția rezultată.

Asta este! La prima vedere, acest circuit este mai dificil precedent. Dar, de fapt, el și mai ușor și mai rapid. Judecător pentru tine:

După cum puteți vedea, în fracțiunea de 0,64, după punctul este în valoare de două numere - 6 și 4. Prin urmare, $ n = 2 $. Dacă eliminați virgulă și zerourile din stânga (în acest caz - un singur zero), vom obține numărul 64. Du-te la al doilea pas: $> => = $ 100, astfel încât numitorul este exact o sută. Ei bine, atunci se poate reduce doar numărătorul și numitorul. :)

Un alt exemplu:

Aici, totul este un pic mai complicat. În primul rând, numere de după virgulă are 3 bucăți, adică, $ N = 3 $, deci va trebui să împartă în 1.000 $ ^> ^> = $. În al doilea rând, dacă eliminăm din zecimal virgulă, vom ajunge aici este: 0,004 → 0004. Reamintim că zerouri pe stânga ar trebui să fie eliminate, astfel încât, de fapt, avem numărul 4. După aceea, totul este simplu: divide, se taie și să obțină un răspuns.

În cele din urmă, ultimul exemplu:

Particularitatea acestei fracțiuni - prezența întregii secțiuni. Prin urmare, de ieșire vom obține fracția necorespunzătoare 47/25. Puteți încerca, cu siguranță, să împartă 47 cu 25, cu un rest și, astfel, realoca o parte a întregului. Dar de ce complica viața ta, în cazul în care se poate face într-o etapă de transformare? Ei bine, se confruntă.

Ce se poate face cu întreaga parte

De fapt, totul este foarte simplu: dacă vrem să obțineți împușcat dreapta, este necesar să se îndepărteze de la ea tot timpul pe o parte a modificărilor, și apoi, când vom obține rezultatul, din nou, să-l adăugați chiar înainte de slash.

De exemplu, ia în considerare același număr: 1,88. Unitate Zabem (partea întreagă) și uita-te la o fracțiune de 0,88. Acesta poate fi ușor transformată:

Apoi, amintiți-vă despre „pierdut“ una din față și adaugă:

Asta este! Răspunsul dovedit la fel ca și că, după separarea întregii ultima dată. Un cuplu mai multe exemple:

Aceasta este frumusetea matematicii: orice fel te duci, dacă toate calculele sunt corecte, răspunsul va fi întotdeauna același :).

În concluzie, aș dori să ia în considerare o altă metodă, care ajută foarte mult.

Transformări „dupa ureche“

Să ne gândim la ceea ce este tot zecimal. Mai precis, așa cum am citit-o. De exemplu, numărul 0.64 - l-am citit ca „punctul zero, 64 sutimi“, nu? Ei bine, sau pur și simplu „64 de cenți.“ Cuvântul cheie aici - „cenți“, adică număr de 100.

Ce zici de 0,004? Același „punctul zero 4000th“ sau pur și simplu „patru miimi.“ Oricum, cuvântul cheie - „miimi“, adică 1000.

Deci, ce e mare scofală? Iar faptul că aceste numere sfârșesc prin „float“, în numitorul celei de a doua faze a algoritmului. Ie 0,004 - un „patru thousandths“ sau „4 împărțit în 1000“:

Încercați să lucreze pentru tine - este foarte simplu. Principalul lucru - pentru a citi corect fotografia originală. De exemplu, 2,5 - un „2 întregi, cinci zecimi“, așa

Și unii 1,125 - sunt "1 întregi, 125,000th," asa

În ultimul exemplu, desigur, cineva va obiecta, spunând că nu fiecare student este evident că 1000 este divizibil cu 125. Dar trebuie amintit că 1000 = 10 = 3 și 10 2 ∙ 5, așa

\ [\ Begin 1000 = 10 \ cdot 10 \ cdot 10 = 2 \ cdot 5 \ cdot 2 \ cdot 5 \ cdot 2 \ cdot 5 = \\ = 2 \ cdot 2 \ cdot 2 \ cdot 5 \ cdot 5 \ cdot 5 = 8 \ cdot 125 \ end \]

Astfel, orice grad de zeci extins doar cu factorul 2 și 5 - acestea sunt factorii pe care trebuie să se uite în numărătorul, astfel încât în ​​cele din urmă toate au căzut.

În această lecție este de peste. Ne întoarcem la o operație feedback mai complicată - vezi „Tranziția de la comun cu fracția zecimală.“.

1. compararea fracțiunilor
2. zecimal repetând
3. Cum de a calcula logaritmi mai repede
4. Adunare și scădere de zecimale
5. Simplifică sarcina deciziei printr-o schimbare a variabilei
6. Sarcina B4: Familie de trei persoane care duc la Moscova la Nijni Novgorod

• Pregătirea gratuită pentru examenul de 7 lecții simple, dar foarte util + teme pentru acasă
•