Construirea unei drepte curbă - elipse, parabole și hiperbole, desen pentru elevi
porțiuni separate ale ovaluri sunt curbe de curbură constantă poate fi desenată cu un șubler, și de aceea ele sunt numite curbe circulare. Curbele având o curbură variabilă este trasată prin curbe și curbe drepte menționate. Pentru curbele drepte includ o elipsă, parabolică, hiperbolă, evolventă cerc, cicloidale diverse tipuri, undă sinusoidală, diverse spirale. Multe drepte curbele sunt formate prin secțiunile plane ale diferitelor suprafețe. Astfel, de exemplu, elipsă, parabolic și hiperbolă sunt formate la intersecția planurilor de suprafață ale unghiului conului diferit.
Elipsă. Locul geometric al punctelor în plan, suma distanțelor de la care la două puncte specificate numite focarele, este o constantă, numită elipsă. Există mai multe modalități de a atrage o elipsă. Cel mai comun este o metodă de două cercuri, diametrele care sunt egale cu axele majore și minore ale elipsei. Dacă prin centrul O petrece un diametru arbitrar, atunci intersectează cercul la punctele E, F și G, H. Prin aceste puncte se realizează, linii paralele cu axele elipsei; intersecția acestor două linii definesc punctul K elipsă și L. De obicei, diametrul firului, unul dintre circumferințele de divizare în 12 părți egale.
Să presupunem că doriți să se potrivească o elipsă la un paralelogram. Ia partea inferioară a părții paralelogram pătrat, construit pe piață, și se potrivește în cercul său. Un centru de cerc O va corespunde centrului O „elipsei, diametrul cercului AB ar corespunde cu diametrul conjugat“ B „a elipsei, și așa mai departe. D. Se împarte jumătate din OD diametru, și jumătate din diametrul conjugat O'D“ în părți egale (de exemplu, patru) și se efectuează prin linii de divizare punct paralelă cu AB. Pe liniile respective vor fi punctele corespunzătoare ale unui cerc și o elipsă, de exemplu, E și E“. Se obține prin aceste puncte de linii poligonale înclinate ODO“paralele. In tehnologie, elipsele se găsesc în spițele volantul, in treptele eliptic.
Fig. 1. Construirea unui elipsoid. Construcția elipsei înscris într-un paralelogram
Parabolă. Locul geometric al punctelor în plan echidistant față de un punct dat, care este punctul central, și o anumită linie, din care directricea se numește parabolei. Cel mai adesea necesar să se construiască o parabolă, potrivirea sale direcții diferite directe (Fig. 2a). Pentru a construi un parabole în secțiunea AB diviza segmentele de linie AB și OB la același număr de părți egale, denota puncte de diviziune într-o secvență de 1-5, 1-5; anumite puncte conecta în mod egal și să tangenta curba direct la familia de linii drepte.
Fig. 2. Construcția unei parabole
Puteți construi un parabole din vârful său A și un punct arbitrar B (Fig. 2b). Pentru acest lucru se realizează prin punctul A axa parabolei AC; construi pe ea ADBC dreptunghi; împart laturile dreptunghiului și denotă același ca și în cazul precedent; prin punctele de divizare pe linia AD se realizează segmente paralele cu axa parabolei și împărțirea punctelor de pe linia dreaptă DB, conectat la vârful parabolei A; punctul de intersecție al liniilor care trec prin punctele indicate prin aceleași numere de referință vor fi un puncte parabole (punctele I, II, III).
Hiperbola. Locul geometric al punctelor în plan, diferența dintre distanțele de la care la cele două puncte predeterminate () este o focare valoare constantă, numită hiperbolă. Hiperbola în desen tehnic se găsește în părți de formă conică, trunchiat de avioane. Curba construite tipic folosind metode geometriei descriptive. Metode geometrice de construire a acestei curbe nu se caracterizează prin simplitate; aici este una dintre ele. Pentru a construi laturile unghiului hiperbola AO și OB (asymptotes) și un punct C se face prin acest punct o linie paralelă cu asymptotes (fig. 3). Apoi, trece linia grinzi O1. O2 și t. D., și punctele de intersecție ale razelor liniilor din nou efectuate asimptote paralele la trecerea lor reciprocă la punctele 11 și 21. Aceste puncte sunt puncte de hiperbolă. ramură hiperbolă în timp ce continuă să se apropie de asymptotes, dar aproape niciodată nu se întâlnească cu ei. Există o altă metodă practică de a construi o hiperbolă.
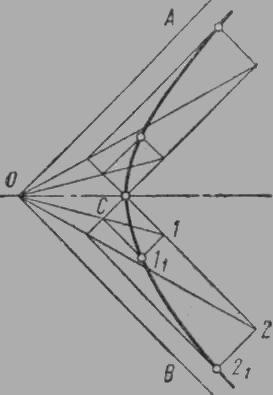
Fig. 3. Construcția hiperbola
Pe site-ul nostru puteți găsi informațiile necesare, detaliate și exacte despre masina Lada Priora - fotografii, descrieri, caietul de sarcini, echipamente de uz casnic mașină de producție, și puteți găsi, de asemenea, recenzii ale automobilelor Lada.