Cum de a găsi cel mai mare divizor comun (GCD)

Luați în considerare două metode de a găsi cel mai mare divizor comun.

Găsirea unui mod de factoring

Primul mod constă în găsirea cel mai mare divizor comun al numerelor de date prin descompunerea în factori de prim.

Pentru a găsi GCD a mai multor numere, suficient pentru a le pune în amorse și să se înmulțească între ei cei care sunt comune pentru toate aceste numere.

Exemplul 1. Găsim GCD (84, 90).

Descompunem numărul 84 și 90 în factori de prim:

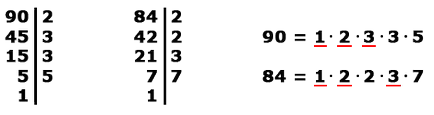
Deci, am subliniat toți factorii principali comuni, rămâne să le înmulțească împreună: 1 · 2 · 3 = 6.

Astfel, GCD (84, 90) = 6.

Exemplul 2. Să ne determina cmmdc (15, 28).

Spread 15 și 28 în factori de prim:

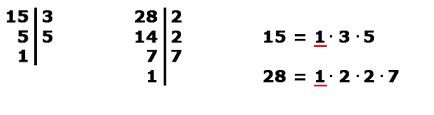
Numerele 15 și 28 sunt relativ prim, ca cel mai mare divizor comun - unitate.

Algoritmul lui Euclid

A doua metodă (altfel aceasta se numește metoda Euclid) constă în găsirea GCD prin divizarea succesivă.

În primul rând, considerăm această metodă, aplicată doar două la numerele, iar apoi vom înțelege cum să-l aplice la trei sau mai multe numere.

În cazul în care cea mai mare dintre cele două numere este împărțit în date minime, numărul de care este mai mic și cel mai mare divizor comun.

Exemplul 1: Ia două numere de 27 și 9. Deoarece 27 împărțit la 9 și 9 este divizibil cu 9, atunci 9 este un divizor comun al numerelor 27 și 9. Acest separator este în același timp și cel mai mare, pentru că 9 nu se poate partaja orice un număr mai mare de 9. Prin urmare, GCD (27, 9) = 9.

În alte cazuri, pentru a găsi cel mai mare divizor comun a două numere utilizând următoarea procedură:

1. Din două numere număr mai mare de date este împărțit în minim.
2. Apoi, un număr mai mic este împărțit de restul care rezultă din divizarea unui număr mai mare de mai puțin.
3. Mai mult, primul reziduu este împărțit într-un al doilea reziduu, care sa transformat dintr-un număr mai mic de diviziune pentru primul reziduu.
4. Al doilea reziduu a fost împărțit în trei, care sunt primite de la prima divizie la un al doilea reziduu și așa mai departe. D.
5. Astfel diviziune continuă atâta timp cât soldul nu se obține zero. Ultimul separator fi doar cel mai mare divizor comun.

Exemplul 2. Să ne găsim cel mai mare divizor comun de 140 și 96:

1) 140. 96 = 1 (44 de reziduuri)

2) 96. 44 = 2 (reziduu 8)

3) 44. 8 = 5 (reziduu 4)

Ultima divizorului este 4 - ceea ce înseamnă că cmmdc (140, 96) = 4.

divizare succesiva poate înregistra coloana:

Pentru a găsi cel mai mare divizor comun a trei sau mai multe dintre aceste numere, vom folosi următoarea procedură:

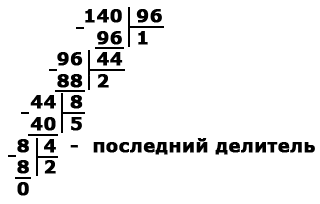
1. În primul rând, vom găsi cel mai mare divizor comun a oricăror două numere de mai multe date.
2. Apoi, vom găsi GCD găsit divizor și o treime din numărul.
3. Apoi am găsit ultima apariție a NOD patrulea divizor și un anumit număr și așa mai departe.

Exemplul 3. Găsim cel mai mare divizor comun de 140, 96 și 48. Numerele GCD 140 și 96, am găsit deja în exemplul anterior (numărul 4). Rămâne de a găsi cel mai mare divizor comun al 4 și o treime din acest număr - 48:

48 împărțit la 4 fără rest. Astfel, GCD (140, 96, 48) = 4.