Cum de a găsi factorul de proporționalitate 1

Coeficientul de proporționalitate (coeficient de proporționalitate liniar) este raportul dintre cele două părți corespunzătoare ale acestor forme. Aceste cifre - o figură de aceeași formă, dar diferite dimensiuni. Coeficientul de proporționalitate este utilizat pentru a rezolva problemele geometrice de bază. Coeficientul de proporționalitate poate fi folosit pentru a calcula lungimile laturilor necunoscute. Pe de altă parte, pe laturile respective pot calcula un factor de proporționalitate. Aceste calcule asociate operației de înmulțire sau simplificarea fracțiilor.

pași Editare

Metoda 1 de la 4:
Calculul factorului de proporționalitate cifre similare Editare

Asigurați-vă că cifrele sunt similare. În aceste cifre toate unghiurile sunt egale, iar părțile sunt legate într-o anumită proporție. Cifrele similare au aceeași formă, dar una peste alta cifra. [1]

• Problema trebuie spus că cifrele sunt similare, sau că acestea au unghiuri egale, sau că părțile sunt proporționale, sau o cifră proporțională cu cealaltă.

Găsiți laturile corespunzătoare ale ambelor piese. Poate fi necesar să se rotească sau flip-una dintre formele pentru a alinia două cifre și de a determina partea corespunzătoare. De obicei, sarcinile sunt lungimile respective ale părților; În caz contrar, măsurați-le. [2] Dacă nu cunosc valorile cel puțin două dintre părțile implicate, este imposibil de a găsi un factor de proporționalitate.

• De exemplu, având în vedere un triunghi a cărui bază este egală cu 15 cm, și un triunghi similar cu baza de 10 cm.

Înregistrare atitudine. Fiecare pereche are două cifre similare factorul de proporționalitate unul este utilizat pentru creșterea mărimii, iar celălalt - cu scăderea. Dacă dimensiunea la cifra crește până la o dimensiune mai mare de bucăți, utilizează raportul: factorul de proporționalitate = (partea mai mare în figură) / (cifre secundare mai mici). Dacă rezoluția mai mare este redus la bucăți bucăți mai mici, utilizează raportul: factorul de proporționalitate = (latura la figuri) / (figura laterală mai mare). [3]

• De exemplu, dacă un triunghi cu o bază de 15 cm, este redus la un triunghi cu o bază de 10 cm, utilizând raportul: = factorul de proporționalitate (cifre secundare mai mici) / (figura laterală mai mare).
  Substituind valorile corespunzătoare, veți obține: coeficientul de proporționalitate = 15 octombrie >>.

Simplificați atitudine. Raportul simplificată (fracție) este un coeficient de proporționalitate. Când reducerea dimensiunii factorului de proporționalitate este o fracțiune adecvată. [4] Prin creșterea dimensiunii coeficientului de proporționalitate este un număr întreg sau fracțiune necorespunzătoare, care poate fi transformată în zecimal.

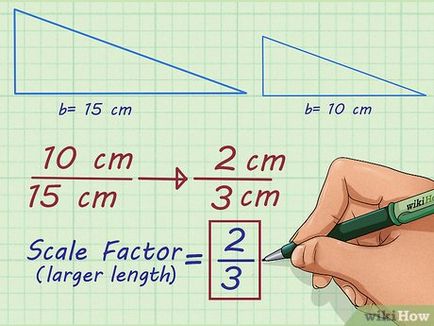
• De exemplu, raportul din 15 octombrie este simplificată la 2 >> 3 >>. Astfel, factorul de proporționalitate a două triunghiuri cu bazele de 15 cm și 10 cm este 2 3 >>.

Problema 1. Găsiți un factor de proporționalitate similar cu următoarele figuri: dreptunghi cu o lățime de 6 cm și un dreptunghi cu o lățime de 54 cm.

• Raportul de înregistrare bazat pe cele două lățimi. Prin creșterea raportului de mărime poate fi scrisă astfel: câștig proporțional = 6 54 >>. Când reducerea raportului dimensiune poate fi scrisă astfel: câștig proporțional = 6 54 >>.
• Simplificați atitudine. 6 54 >> raport simplifică 1 septembrie = 9> = 9>. 6 54 >> raport simplifică 1 septembrie >>. Astfel, factorul de proporționalitate a două patrulatere este de 9 sau 1 9 >>.

Problema 2. Side poligon neregulat este egală cu 14 cm. Side astfel de poligon este de 8 cm. Găsiți un factor de proporționalitate.

• Cifrele greșite sunt similare în cazul în care toate părțile lor sunt proporționale. Astfel, coeficientul de proporționalitate poate fi calculată în conformitate cu orice valoare cunoscută. [6]
• Deoarece laturile corespunzătoare ale poligoanelor sunt cunoscute, putem scrie raportul. Atunci când creșterea raportului de mărime poate fi scrisă ca: = un factor de proporționalitate la 14 august >>. Atunci când reducerea raportului dimensiune poate fi scrisă ca: = un factor de proporționalitate la 14 august >>.
• Simplificați atitudine. 14 august >> relație simplifică la 7 4 = 1 3 4 = 1. 75> = 1> = 1,75>. 14 august >> relație simplifică 4 iulie >>. Astfel, factorul de proporționalitate a două poligoane neregulate sau egal cu 1. 75 >> 7 aprilie.

Problema 3. Laturile ABCD dreptunghi sunt 8 cm și 3 cm. Dreptunghi EFGH este dreptunghi mare și altele asemenea. Găsiți zona efgh dreptunghi, în cazul în care coeficientul de proporționalitate este egal cu 2,5.

• Înmulțiți lățimea ABCD dreptunghi pe factorul de proporționalitate. Veți găsi lățimea dreptunghiului efgh 3 × 5 = 2. 7. 5.
• Înmulțiți lungimea ABCD dreptunghi pe factorul de proporționalitate. Veți găsi lungimea efgh dreptunghi de 8 x 2. 5 = 20.
• Inmultiti lungimea și lățimea EFGH dreptunghi pentru a găsi zona sa: 7. 5 x 20 = 150. Astfel, suprafața de EFGH dreptunghi egal cu 150 de centimetri pătrați.