Cum de a găsi o zonă în secțiune transversală a cilindrului

Secțiunea transversală a cilindrului cu un plan care trece prin baza sa este întotdeauna un dreptunghi. Dar, în funcție de locație, aceste casete vor fi diferite. Găsiți o arie în secțiune transversală axială, perpendicular pe baza cilindrului. O parte a dreptunghiului este egală cu înălțimea cilindrului, al doilea - diametrul cercului de bază. Prin urmare, aria secțiunii transversale, în acest caz, va fi egală cu produsul dintre laturile dreptunghiului. S = 2R * h, unde S - aria secțiunii transversale, R - condiții raza cercului de bază, predeterminate ale problemei și h - înălțimea cilindrului, de asemenea, predeterminate condiții ale problemei.

Dacă secțiunea transversală perpendiculară pe baze, dar nu trece prin partea axei de rotație a dreptunghiului nu este egal cu diametrul cercului. Acesta trebuie să fie calculată. Pentru a face acest lucru în ceea ce privește problema de a fi spus la ce distanță față de axa de rotație a planului de secțiune se extinde. Pentru computațională comoditate construi cerc de bază cilindru, raza slide si se pune deoparte pe ea distanța pe care secțiunea transversală din centrul cercului. Din acest punct de glisează cu raza normalelor până la intersecția lor cu cercul. Conectați punctele de intersecție cu centrul. Trebuie să găsești mărimea coardei. Găsiți dimensiunea de jumătate coarda teorema lui Pitagora. Acesta va fi egală cu rădăcina pătrată a diferenței pătratelor raza cercului și distanța de la centrul la linia de secțiune. a2 = R2-b2. Toate coardă este, prin urmare, egal cu 2a. Se calculează aria secțiunii transversale care este egală cu produsul dintre laturile dreptunghiului, adică, S = 2a * h.

Cilindrul poate fi tăiat și planul nu trece prin planul bazei. În cazul în care secțiunea transversală se extinde perpendicular pe axa de rotație, acesta va fi un cerc. Suprafața sa în acest caz este de bază pătrată, care se calculează cu formula S = πR2.

Pentru a rezolva această problemă, trebuie să vă amintiți că un astfel de trunchi de con, și ce proprietăți le posedă. Asigurați-vă că pentru a face un desen. Acest lucru va determina ce formă geometrică este o secțiune a conului. Este foarte posibil ca, după soluționarea problemei nu va fi prezent pentru tine dificultate.

cone rotundă - corp obținut prin rotirea triunghiului în jurul unuia dintre celelalte două laturi. Direct emanată de la vârful conului și se intersectează baza sa, numită generatoare. Dacă toate generatoarele sunt egale, atunci conul este dreaptă. La baza unui con circular este un cerc. Perpendicular a scăzut de la vârful la baza, o înălțime a conului. La înălțimea conului circular dreapta coincide cu axa. Axa - o linie dreaptă care leagă partea de sus la baza centrului. Dacă planul de tăiere orizontal a conului circular este paralel cu baza, baza sa superioară este un cerc.

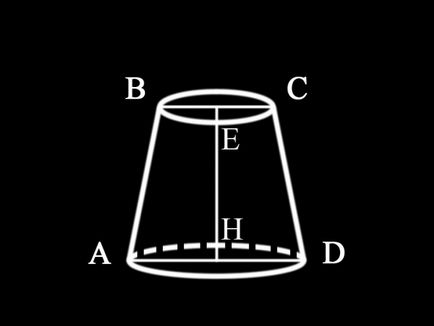
Deoarece declarația problemă nu este specificat ce fel de con este dată în acest caz, putem concluziona că acesta este tot de trunchi de con drept, a cărui secțiune orizontală este paralelă cu baza. secțiune axială, adică plan vertical care trece prin axa circulară trunchi de con. Este un trapez isoscel. Toate Axial secțiune transversală a conului din dreapta rotund sunt egale. Prin urmare, pentru a găsi aria secțiunii axiale. necesare pentru a găsi zona trapezului, bazele pentru care sunt diametrele bazelor tronconice. și părțile laterale - generatoarele sale. Înălțimea trunchiului de con este, de asemenea, înălțimea trapezului.

Aria trapezului este definită prin formula: S = ½ (a + b) h, unde S - suprafața trapezului; a - valoarea bazei inferioare a trapezului; b - valoarea bazei sale superioare; h - înălțimea trapezului.

Deoarece condiția nu este specificat exact care valorile sunt date, se poate presupune că diametrele atât baza și înălțimea trunchiului de con sunt cunoscute: AD = d1 - diametrul bazei inferioare a trunchiului de con; BC = d2 - diametrul bazei sale superioare; EH = h1 - înălțimea conului .tak fel, aria secțiunii axiale a unui trunchi de con definit: S1 = ½ (d1 + d2) h1

• zonă a unui trunchi de con

Cilindrul este o figură spațială, și este formată din două baze egale, care sunt cercuri și linii de legătură suprafață laterală care delimitează baza. Pentru a calcula ploschadtsilindra. Găsiți aria suprafeței sale, și să le ori.

• line;
• Calculator;
• Conceptul de zonă și circumferința unui cerc.

Se determină suprafața bazelor cilindrilor. Pentru a măsura aceasta, folosind un diametru al bazei conducător, și apoi se împarte la 2. Acesta este raza bazei cilindrului. Se calculează suprafața unei baze. În acest scop, ridicați valoarea razei sale în pătrat și se înmulțește cu un π constant, Skr = π ∙ radicalul R, unde R - raza cilindrului. și π≈3,14.

Ia suprafața totală a celor două baze, în baza definiției buteliei. care spune că baza sa egale între ele. Zona de un cerc de bază se înmulțește cu 2 Sosn ∙ Skr = 2 = 2 π ∙ ∙ radicalul R.

Se calculează aria suprafeței laterale a cilindrului. Pentru a obține această circumferință, care limitează una din bazele cilindrilor. Dacă raza este deja cunoscut, atunci se calculează prin înmulțirea numărului de 2 până la π și de bază raza R, l = 2 π ∙ R ∙, unde l - lungimea cercului de bază.

Se măsoară lungimea cilindrului. care este egală cu lungimea segmentului care leagă punctele de bază respective sau centre. În convențional cilindru directă generatoarea L este numeric egală cu H. înălțimea sa calculează aria suprafeței laterale a cilindrului. înmulțirea lungimii sale prin formarea unei Sbok = 2 ∙ π ∙ R ∙ L. bază

Se calculează suprafața cilindrului. însumarea baze pătrate și suprafață laterală. S = + Sosn Sbok. Valori Substituind suprafețe definibile obține S = 2 ∙ π ∙ + 2 radicalul R ∙ π ∙ R ∙ L, scoate factorul comun S = 2 ∙ π ∙ R ∙ (R + L). Acest lucru permite calcularea suprafeței unui cilindru cu o singură formulă.

De exemplu, diametrul bazei cilindrului directe de 8 cm, iar înălțimea este de 10 cm. Se determină suprafața suprafeței sale laterale. Se calculează raza cilindrului. Acesta este egal cu R = 8/2 = 4 cm. Drept cilindru generatoarea egală cu înălțimea acesteia, adică L = 10 cm. Calculele folosesc o singură formulă, este mai convenabil. Apoi, S = 2 ∙ π ∙ R ∙ (R + L), înlocuirea corespunzătoare numerice valorile S = 2 ∙ 3,14 ∙ 4 ∙ (4 + 10) = 351.68 cm².