Cum se calculează rata dobânzii efective
Cum se calculează rata dobânzii efective
De fapt, sensul ratei dobânzii efective este destul de simplu - este conceput pentru a reflecta costul real al creditului la punctul de vedere al debitorului, adică, să ia în considerare toate plățile sale secundare direct legate de credit (altele decât plățile pe împrumut în sine). De exemplu, astfel de plăți secundare sunt notorii taxe „ascunse“ bancă - taxe pentru deschiderea și întreținerea conturilor pentru primirea de numerar în numerar, etc. Un alt exemplu: Dacă luați un credit auto, banca se angajează să asigure ați achiziționat mașina pentru întreaga perioada de creditare. În acest caz, de asigurare va fi obligatorie pentru tine de partea de plăți (deși nu banca în sine, și societățile de asigurare) .Ce este interesant, Banca Centrală, băncile comerciale sunt obligate să dezvăluie rata efectivă a dobânzii la împrumuturi și chiar oferă formula de calcul sa nu indică ce specifică plăţile ar trebui să fie incluse în acest calcul. Ca urmare, diferite bănci au puncte de vedere diferite în această privință: mulți, de exemplu, nu sunt incluse în calculul ca plățile de asigurare de timp.
Cu toate acestea, cea mai corectă și arată ca abordarea pe care în calcularea ratei dobânzii efective include toate taxele care sunt necesare pentru a obține acest împrumut. În special, toate plățile de asigurare obligatorii.
După ce a tratat această problemă, suntem acum în măsură să dea o definiție strictă a ratei dobânzii efective.
Rata dobânzii efective - este o rată a dobânzii complexă calculată pe baza ipotezei că toate plățile necesare pentru a obține acest împrumut, du-te la răscumpărarea lui.
Aceasta este, în cazul în care rezultatul mărimea creditului S0 debitorul este obligat să efectueze plăți R0. R1. R2. .rn la momentele de timp t0 = 0, t1. t2. tn respectiv (care include atât plățile pe împrumut în sine și partea Comisiei, plățile de asigurare, etc.), rata efectivă a dobânzii am găsit de relația
.
Rata dobânzii efective este utilizat în principal pentru compararea diferitelor oferte bancare, precum și calculul său de data exactă a plăților de comision sunt, de obicei necunoscute. Prin urmare, în cazul în care plățile sunt efectuate printr-un interval formal egale de durata de timp # 964; (Lunar, trimestrial, etc.), atunci (1) devine:
.
În cazul în care împrumutatul toate plățile, cu excepția, poate, chiar primul, același (R1 = R2 = = Rn = R.), Apoi, în conformitate cu formula calcularea sumei unei relații geometrice finite pentru determinarea ratei dobânzii efective va fi:
.
Din păcate, găsirea valoarea exactă a ratei dobânzii efective, chiar și în acest caz, relativ simplu este imposibil, deci trebuie să-l selectați (cel mai bun mod - folosind o metodă numerică specială). Cum anume - acest lucru va fi discutat în continuare.
Pentru creditul cu următoarele condiții:
- credite pe termen - 3 ani;
- Rata dobânzii (o vom nota cu j) - 18% pe an;
- schema de rambursare - lunar egal (fix) la cheltuieli;
- pentru taxa de acord de împrumut - 1% din suma;
- taxă lunară pentru menținerea contului de împrumut - 0,1% din valoarea creditului
Rata efectivă a dobânzii ar fi 22,8%. Pentru a testa găsi valorile tuturor variabilelor prezente în Formula (3):
- R0 = 0,01 × S0;
- n = 36;
- # 964; =;
- j = 0,18;
- plata anuitate :;
- R = A + 0,001 x S0 ≈ 0,0372 × S0;
- i = 0228;
- rata dobânzii efective lunare IM = (1 + i) # 964; ≈ 1,017262.
Înlocuind aceste valori în formula (3), după o reducere a S0 ușor pentru a verifica validitatea egalității (cu excepția cazului, desigur, a ignorat eroarea de rotunjire):
.
O metodă generală pentru calcularea ESR
Deci, am observat că mărimea ratei efective a dobânzii, chiar și pentru operațiunile relativ simple de împrumut nu poate fi găsit folosind o formulă. Aici vin în ajutorul așa-numitelor metode numerice. care permit un număr finit de pași pentru a calcula valoarea aproximativă a cantității necunoscute cu precizia necesară.
O metodă generală pentru calcularea aproximativă a ratei dobânzii efective, care vor fi discutate în continuare, poate fi aplicată pentru orice împrumuturi, plățile pentru care se efectuează la intervale regulate. Baza sa este o metoda Newton numerică. esența care, în termeni generali, este după cum urmează.
Să presupunem că trebuie să găsim o soluție pentru ecuația f (x) = 0, unde f (x) - o funcție diferențiabilă. Apoi, în anumite condiții, o secvență de numere x (k)>, care este prima valoare x (0) este selectat în mod independent, și fiecare formulă următoare situat
,
converge la soluția exactă a acestei ecuații. Noi suntem acum, indiferent de condițiile, puteți găsi cu ușurință dacă doriți informații despre limitările metodei lui Newton.
Să vedem acum cum să folosească această metodă pentru a calcula rata dobânzii efective.
Vom introduce o nouă valoare v # 964; = (1 + i) - # 964;. care se numește factorul de reducere pentru perioada de timp # 964;. Cu ajutorul formulei (2), reprezentând raportul global pentru a găsi un interes eficient poate fi rescrisă după cum urmează:
.
Găsirea rădăcina acestei ecuații este echivalentă cu găsirea funcției rădăcină
.
Această funcție are doar o singură rădăcină pozitivă (ne interesează doar rădăcinile pozitive), și se află în intervalul (0, 1). Această rădăcină poate fi ușor de găsit prin utilizarea metodei lui Newton, pre-calcul derivata funcției f (x):
.
Acum, alegând o aproximare x inițială (0) = 1, cu formula (4), obținem o secvență de numere x (k). convergente la valoarea exactă a v # 964;. O valoare aproximativă a ratei dobânzii efective necunoscută se constată din următoarea relație:
(Presupunând că am terminat calculul numărului etapa n).
Rata dobânzii efective pentru dimensiunea creditului S0 = 1000 £ Marea Britanie, a emis în anul sub simplu rata dobânzii j = 20%. Împrumutat pentru a rambursa împrumutul au fost efectuate următoarele plăți parțiale:
- R1 = 600 livre după 3 luni (t1 = ¼) după începerea tranzacției;
- R2 = 310 livre după 9 luni (t2 = ¾) după începerea tranzacției;
- R3 = 194,25 de lire sterline pe an (t3 = 1), după începerea tranzacției.
Deoarece perioada de timp # 964; selectați un bloc (# 964; = ¼). În conformitate cu metoda descrisă mai sus, introducem o funcție auxiliară
și pentru a găsi derivatul său:
Acum, alegând un x inițial de aproximare (0) = 1, cu formula (4) construi o secvență a valorilor aproximative ale discount factorului v # 964; și rata dobânzii efective i:
≈ i 0,21316403087292
Deja în a cincea etapă de calcul a condus la același rezultat ca și în anul precedent, și cu o precizie care este puțin probabil să fie vreodată în stare să aibă nevoie. Acest rezultat este mai mare de 1,3% mai mare decât cea declarată rata dobânzii (nominal) pe împrumut, cu toate că nu a existat nici taxe ascunse sau orice alte plăți suplimentare.
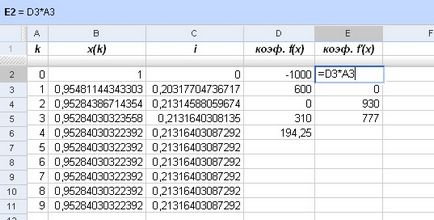
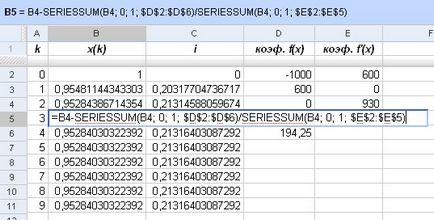
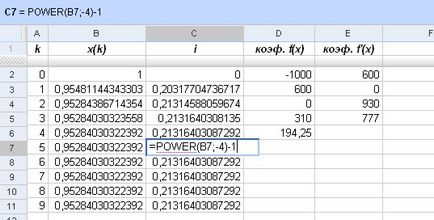
Fiți atenți la următoarele puncte:
Să examinăm acum mai complexe, dar mai recent exemplu.
Împrumut de 24 de mii de euro, a emis doi ani, la 12% pe an, rambursabil în rate lunare, în conformitate cu schema diferențiată. Taxele de aranjament de 1% din suma. În plus, în fiecare lună debitorul va plăti taxa pentru menținerea contului de împrumut de 0,1% din valoarea creditului. Trebuie să găsim o rată a dobânzii efective a creditului.
În primul rând, vom construi graficul de rambursare a creditului (cu excepția structura taxelor). Plățile către rambursare a creditului formează o progresie aritmetică cu termenul inițial
A1 = (+ 0,12 ×) × 24 000 = 1240 euro
- (0,12 x x 24000) x = - 10 euro.
În plus, la primirea împrumutului debitorului a trebuit să plătească 0,01 x 24 = 240 000 euro, și în fiecare lună cu el suprataxă de măsurare 0,001 x 24 = 24 000 de euro. Prin urmare, programul de plăți asupra creditului este după cum urmează:
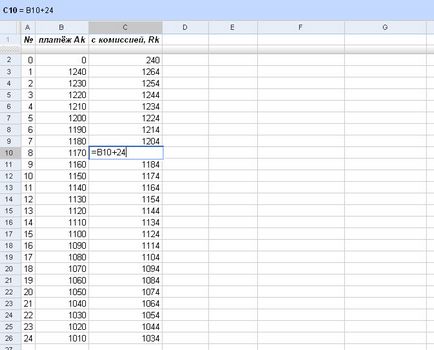
Fig. Programul de plăți pe împrumut
Valorile coloanei „cu comisia, Rk», cu excepția primului (index 0), coincid cu coeficienții puterilor lui x în funcția f (x), pe care le vom folosi în calcule. Pentru primul coeficient (zero grade x) este necesar de la o plată inițială R0 = 240 scădere mărimea creditului (formula la stânga sus):
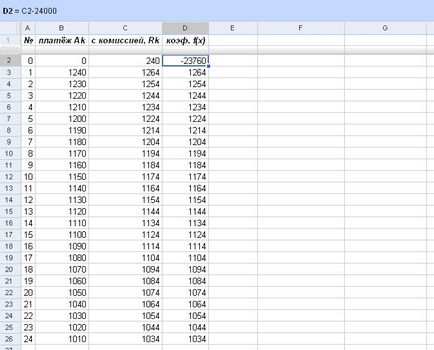
Fig. Găsirea coeficienții funcției f (x)
Coeficienții de puteri ale lui x f derivat „(x) sunt principiul deja cunoscut:
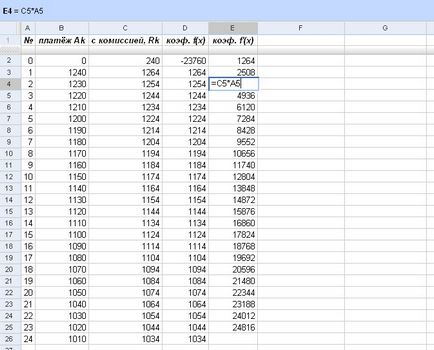
Fig. Găsirea coeficienții f derivat „(x)
Acum, în cele din urmă, puteți folosi metoda lui Newton pentru a găsi un factor de reducere lunar (cu formula în colțul din stânga sus):
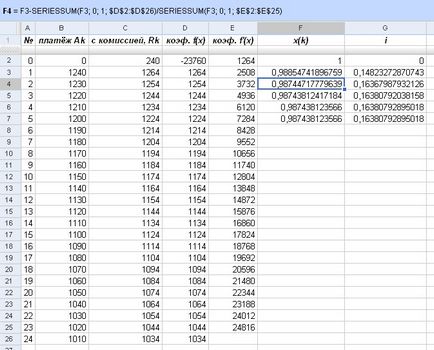
Fig. Găsirea unui factor de reducere lunar
Concomitent cu calcularea factorului de actualizare lunară se definesc rata efectivă a dobânzii i:
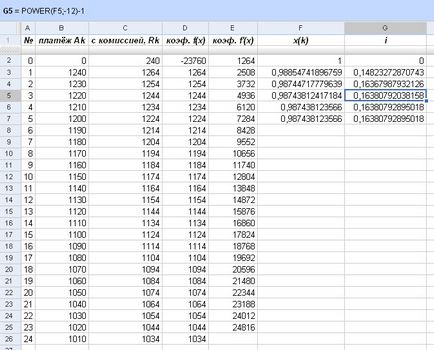
Fig. Găsirea ratei dobânzii efective
Ca și în exemplul din paragraful anterior, metoda lui Newton ne-a condus la răspunsul final la doar cinci calcule: rata efectivă a dobânzii la împrumutul în cauză este aproximativ egală cu 16,38%, 4,38% mai mare decât rata nominală.
Calculul EPS pentru anuitate
Metoda pe care le-am considerat mai sus, atunci când sunt utilizate corect, este destul de convenabil. Dar, în anumite cazuri, și anume, pentru schema de anuitate rambursare a împrumutului, rata dobânzii efective pot fi găsite chiar mai repede și mai ușor. De fapt, principalul avantaj al metodei care va fi discutată în continuare, este mai compact.
Rescrie (3) - raportul pentru a determina rata dobânzii efective, ceea ce este valabil pentru rambursare a plăților anuitate de împrumut - folosind deja familiar pentru noi factorul de actualizare v # 964; = (1 + i) - # 964; :
.
apoi, folosind formula (4) poate fi o secvență de numere x (k)>, se apropie de valoarea exactă factor de actualizare v # 964; .
Rata efectivă a dobânzii pentru împrumutul din primul exemplu. Termenii amintesc, au fost următoarele:
- credite pe termen - 3 ani;
- Rata dobânzii j - 18% pe an;
- schema de rambursare - lunar egal (fix) la cheltuieli;
- pentru taxa de acord de împrumut - 1% din suma;
- taxă lunară pentru menținerea contului de împrumut - 0,1% din valoarea creditului.
În plus, pentru a fi specific, presupunem că mărimea împrumutului este de 12 milioane. Ruble.
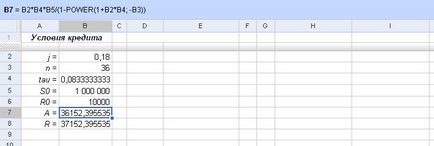
Fig. Adăugarea la condițiile inițiale
Următorul pas - este calculul coeficienților funcției f (x):
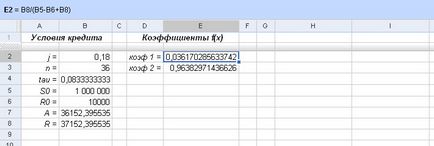
Fig. Calculul coeficienților f (x)
Primul coeficient în combinație este o aproximare inițială a x (0). Trageți-l în celula corespunzătoare și metoda lui Newton calculează numărul de luni de aproximări factor de actualizare (observați cu formula în colțul din stânga sus):
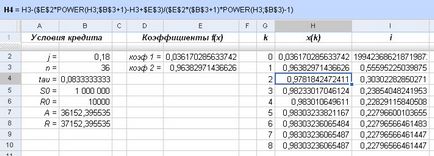
Fig. Calcularea factorului de actualizare lunar
În același timp, vom calcula valoarea aproximativă a ratei efective a dobânzii i:
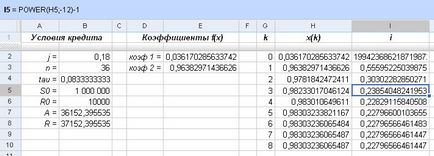
Fig. Calculul ratei dobânzii efective
După cum puteți vedea, după opt calcule, ne-am confirmat încă o dată că rata efectivă a dobânzii la împrumutul în cauză este de aproximativ 22,8%, cu 4,8% mai mult decât valoarea nominală.
Notă. După umplerea unei matrițe similară cu cea prezentată în figuri, veți putea apoi să determine instantaneu rata efectivă a dobânzii la orice împrumut este rambursat în conformitate cu schema de anuitate, numai schimbarea condițiilor inițiale.
În concluzie, vreau să fac o altă importantă observație generală. Am considerat metoda este garantata de a converge (de exemplu, să conducă la valoarea dorită a factorului de actualizare și rata dobânzii efective), în cazul în care valoarea inițială a valorii selectate (7). Dacă luăm în considerare o altă aproximare inițială, metoda poate converge la a doua rădăcină a funcției f (x) - o unitate (corespunzătoare valorii ratei dobânzii efective este zero). De exemplu, în exemplul avem în vedere, sa întâmplat, vom lua ca o aproximare inițială, orice număr mai mare de 0.992.
Și încă o observație generală cu privire la alegerea unei metode numerice. Există o mare varietate de metode numerice, dintre care multe ar putea fi bine aplicate pentru a rezolva problemele noastre. Metoda lui Newton a fost ales pentru că este, în opinia noastră, un echilibru între utilizarea vitezei de complexitate și de convergență (vă amintiți, suntem într-unul din exemplele nu au făcut mai mult de opt calcul). Sunt mai rapide, dar sunt mai greu de înțeles metode. Există metode mai simple, cu mai puține restricții și convergența garantată, dar necesită o cantitate mare de calcul. De exemplu, dacă am fi folosit în ultimul exemplu, o metodă bine-cunoscut de repetare simplu. în scopul de a obține acuratețea necesară, ne-ar trebui să facă o sută de calcule. Este clar că aceste calcule face încă programul.