învăța să program

În cazul în care toți minorii matritsyAporyadkakravny zero, atunci toți minorii de ordin k + 1, în cazul în care acestea există, de asemenea, sunt egale cu zero.
Rangul matritsyA numit minori de ordin maximale ale matricei A. nenul.






Rangul maximă poate fi egal cu numărul minim de rânduri sau numărul de coloane ale matricei, adică, dacă matricea are o dimensiune de 4x5, gradul maxim va fi de 4.
Cel puțin rangul unei matrice este egal cu 1, dacă nu se face cu o matrice de zero, există întotdeauna un rang egal cu zero.

Rank-order matrice pătratică nesingular n este egal cu n, deoarece este un determinant minor de ordinul n și matricea nesingular este diferit de zero.
Transpunerea matricei nu schimbă rangul său.

Să rangul matricei este. Apoi, orice minor de ordine, diferit de zero, se numește minor de bază.
Exemplu. Date fiind matricea A.

Determinantul matricei este egal cu zero.
a doua ordine minore. Prin urmare, r (A) = 2 și baza minoră.
Baza minoră este, de asemenea, un minor.
Minor, deoarece = 0, deci nu va fi de bază.
Sarcină. să verifice în mod independent, ceea ce alți minori de ordinul al doilea sunt de bază și care nu sunt.

Găsirea rangul unei matrice prin calcularea tuturor minorilor sale necesită prea multă muncă de calcul. (Cititorul poate verifica dacă în a patra comandă pătrat matrice de 36 de minori de ordinul doi.) Prin urmare, un algoritm diferit este folosit pentru a găsi rangul. Pentru a descrie această nevoie de informații suplimentare.

Noi numim acești pași matrice elementare asupra lor:
1) schimbarea rânduri sau coloane;
2) înmulțirea rândul sau coloana numărul de non-zero;
3) adăugarea la una dintre liniile altui rând înmulțit cu numărul sau adăugarea uneia dintre coloanele din cealaltă coloană, înmulțit cu un număr.

Atunci când nu rang matrice elementar se schimbă.
Algoritmul de calcul rangul unei matrice similar cu algoritmul de calcul al determinantul, și este că, cu ajutorul matricei elementare este redusă la o formă simplă pentru care pentru a găsi rangul nu este dificil. Deoarece pentru fiecare grad de conversie nu este schimbat, apoi prin calcularea rangul matricei transformat, vom găsi astfel rangul matricei originale.

Să presupunem că doriți să calculeze gradul de dimensiunile MXN matricei.

1. Cu permutare de rânduri și coloane care doresc să se asigure că colțul din stânga sus al matricei a fost elementul non-zero. Deci, noi credem că. Primul rând lăsând neschimbat.
2. A doua linie vom adăuga primul, înmulțit cu numărul.
3. Pentru a adăuga al treilea rând din primul rând înmulțit cu numărul.
4. Procesul continuă până când, până când vom obține un zero pe primul loc în ultimul rând. Rezultatul este o matrice A1, în care într-o primă coloană toate elementele sunt 0, cu excepția membru.

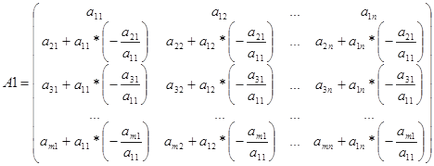
A1 matrice calcule are forma

1. Dacă toate rândurile începând de la al doilea, rezultând într-o matrice de zero, atunci rangul său este egal cu 1, deoarece nu sunt minore primul nenul ordin. În caz contrar, permutare de rânduri și coloane cu unități de numere mai mari, atingerea celui de al doilea element al doilea rând este nenul. Deci, noi credem că.
2. În primul rând și de rezervă a doua linie de neschimbat.
3. Pentru a adăuga a treia linie de-a doua înmulțit cu numărul. Rezultatul este acela că al doilea element al treilea rând este zero.
4. Apoi vom adăuga a patra linie de-a doua înmulțit cu numărul etc. Rezultatul este o matrice

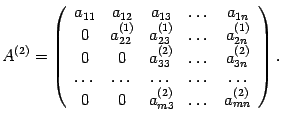
Dacă toate rândurile de la al treilea, zero, ca fiind minor. În caz contrar, permutare de rânduri și coloane cu numere mai mari de două, se face la al treilea element al treilea rând este nenul. În plus, adăugarea a treia linie, înmulțit cu numărul corespunzător pe rândurile pentru a obține un număr mare de zerouri în coloana a treia din al patrulea element, etc.
La un moment dat am ajuns la matricea în care toate liniile începând cu (+ 1 r) -lea. sunt zero (sau absente la) și minor în primul rând și prima coloană este determinantul unei matrice triunghiulare cu elemente diagonale nenule. Rangul unei matrice este egal. În consecință, Rang (A) = r.

În algoritmul propus pentru identificarea gradului de matrice toate calculele trebuie să fie efectuate fără rotunjire. Samavolnic mică schimbare în cel puțin unul dintre elementele matricei intermediar poate conduce la faptul că răspunsul obținut va fi diferit de rangul matrice originală în mai multe unități.
Dacă elementele matricei originale sunt numere întregi, atunci calculul este convenabil realizat fără utilizarea fracțiunilor. Prin urmare, la fiecare pas, este recomandabil să se multiplice numerele de linie, astfel încât, atunci când nu apar calculele fracții.

În laborator și lucrări practice, considerăm un exemplu atunci când un rang al unei matrice.

Algoritmul pentru găsirea unei norme matrice.
Alocați doar trei norma matrice.
Prima matrice norma = maximă a numerelor obținute în adăugarea tuturor elementelor fiecărei coloane, modulo luate.
Exemplu: Fie matricea 3x2 O dimensiune dată (Figura 10). În prima coloană sunt elementele 8, 3, 8. Toate componentele sunt pozitive. Am găsit suma lor: 8 + 3 + 8 = 19. În a doua coloană sunt elementele 8, -2, -8. Două elemente - negative, astfel încât adăugarea acestor numere, este necesar să se înlocuiască modulul aceste numere (adică, fără un „minus“ semn). Am găsit suma lor: 8 + 2 + 8 = 18. Valoarea maximă a două numere - este 19. Deci, prima regulă a matricei este egală cu 19.

A doua regulă a matricei este rădăcina pătrată a sumei pătratelor tuturor elementelor matricei. Și înseamnă că cuadratura toate elementele matricei, și apoi adăugați în sus valorile obținute din rezultatul rădăcină pătrată.
În cazul nostru, 2 norme de matrice sunt egale cu rădăcina pătrată a 269. În diagrama, am învățat aproximativ rădăcina pătrată din 269, și ca urmare a primit aproximativ aproximativ 16.401. Deși mai corect nu extrage rădăcina.

O a treia normă a matricei este un număr mai mare obținut prin adăugarea elementelor din fiecare rând, modulo luate.
În exemplul nostru, elementele de primă linie sunt: ​​8 8. Toate elementele pozitive. Vor găsi suma lor: 8 + 8 = 16. În al doilea rând elemente sunt: ​​3, -2. Un element este negativ, astfel încât adăugarea acestor numere, este necesar să se substituie modulul acel număr. Am găsit suma lor: 3 + 2 = 5. A treia linie stativ elemente 8 și -8. Un element este negativ, astfel încât adăugarea acestor numere, este necesar să se substituie modulul acel număr. Vor găsi suma lor: 8 + 8 = 16. Valoarea maximă a acestor trei numere - este 16. Deci, a treia norma a unei matrice este egal cu 16.

Compilat Saliy NA