Line și plan, geometrie descriptivă
Semne linie și paralelism plan au următoarea definiție - linia m paralel cu planul α, dacă în planul α se poate trage o linie dreaptă n, paralel cu m:
\ [(M ║ n) ∧ (n ⊂ α) → ║ α m \]
Evident, printr-un spațiu punct care nu face parte din planul poate deține un set infinit de linii paralele cu planul dat.
Prin punctul A trage o linie dreaptă m. paralel cu planul α. predeterminate intersectând linii a și b
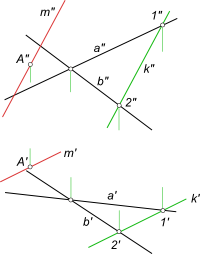
Criterii de paralelism a liniei drepte și plane
Dacă nu există condiții suplimentare, atunci putem, folosind semnele liniei paralele și planul. dețin oricare dintr-o pluralitate de linii drepte care trec prin punctul A și paralelă cu planul a - de exemplu, paralel cu una direct sau b. Dacă am pus condiția ca linia nu este paralelă cu liniile a și b - este necesar pentru a construi o linie de 12 și mențineți m dorită directă (m`, m „), paralel cu aceasta.
După un punct predeterminat A trage un plan paralel cu linia f

Criterii de paralelism a liniei drepte și plane
planul Intersectând este stabilit la un punct A și b drepte. În acest caz, una dintre liniile (linia a) paralelă cu linia f.
După un punct predeterminat K trage o linie dreaptă paralelă cu planul triunghiului ABC și linia frontală care trece prin vârful A
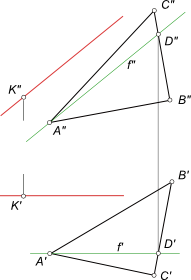
Criterii de paralelism a liniei drepte și plane
Am construit frontal f pentru o anumită condiție - prin A` și paralel cu firul axa x drept f`. Această linie intersectează B`C` - latură a triunghiului de la d`. Prin link-ul găsi vedere frontală D „punctul deținut D. partea BC a triunghiului. Trasez prin punctele A“ și D „drept f“. Prin punctul K trage o paralelă directă cu frontal f. Aceasta este o paralelă directă cu planul triunghiului și ABC.
Prin punctul A (-3; 4; 3) trage o linie dreaptă paralelă cu cele două planuri α (3x + 4y-2z + 7 = 0) și β (x-2z + 5 = 0)
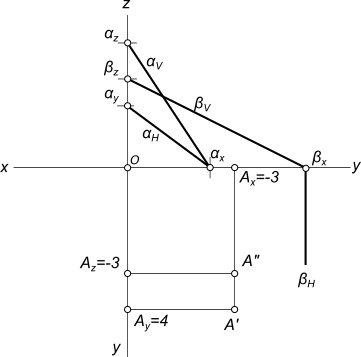
Criterii de paralelism a liniei drepte și plane
1. Construirea o proiecție a punctului A 2. realizează urme plane α (3x + 4y-2z + 7 = 0): a) z = 0; 3x + 4y + 7 = 0; αH; y = 0; 3x + 7 = 0, x = -7/3, x = -2,33; b) y = 0; 3x-2z + 7 = 0; av; x = 0; 2Z + 7 = 0, z = 3,5; z = 0; 3x + 7 = 0, x = -2,33 3) este construit după cum urmează planul β (x-2z + 5 = 0): βV x = 0; 2Z + 5 = 0, z = 5/2, z = 2,5; z = 0; x + 5 = 0, x = -5 4) Construirea linia de intersecție a avioanelor α definit 1-2 și β
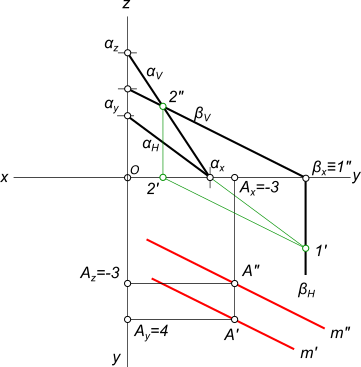
Criterii de paralelism a liniei drepte și plane
5) Construirea liniei m plane paralele a și p: m`‖1`-2` și m "‖1" -2 "