Minunat triunghi Blaise Pascal, matematica, pe care îmi place
Toți știu despre triunghiul lui Pascal în tinerețe. Dar, aparent, nu știu toate minunile care conține un triunghi. De fapt, suntem încă descoperi lucruri noi!
Construite un triunghi este destul de ușor: pe marginile exterioare nevoie pentru a pune unitatea, și fiecare număr interior este suma celor două numere, care stau deasupra ei. Astfel, al treilea număr în al șaselea rând se datorează faptului că este suma numerelor și.
Atenție! De fapt, noi spunem că este al doilea număr, în al cincilea rând. Din motive care vor deveni clar în curând, vom începe să numeri rândurile și coloanele unui triunghi de la zero. De exemplu, al doilea număr este egal cu a patra linie.
Cunoscând regula plus, este fără sfârșit: puteți scrie cât mai multe linii ca și răbdare va permite.
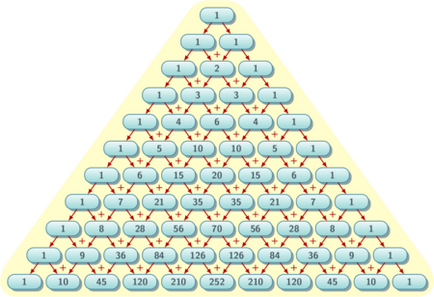
Primele 10 rânduri de triunghiul lui Pascal
Pascal a introdus triunghiul în 1653 în Traité du triunghi arithmétique, ca parte a studiului de probabilitate și de calcul. Sarcinile au fost de aproximativ după cum urmează: „Dacă vreau să selectați două persoane din cele patru date cât există posibile perechi«»sau“ Care este probabilitatea de a avea o casă plină Când cinci cărți (notă de poker trei cărți de un rang și două dintre ele.) de la punte, care este bine amestecat? „“ Pascal și Fermat discutat, în principal probabilitatea de scrisori schimbate în momentul respectiv. Puteti vedea sursa triunghiul lui Pascal aici.
Cum triunghiul este asociat cu o probabilitate? Ei bine, dacă doriți să selectați obiecte din baza de date, numărul de opțiuni posibile este egal cu numărul din rândul-lea-lea al triunghiului. Amintiți-vă că siruri de caractere și numere de numere din liniile de triunghi începe de la zero! Folosind această regulă, vom vedea că există exact două moduri de a alege o persoană din cele patru date. Și astfel - al treilea număr din linia nouă a triunghiului, atunci nu există nici o modalitate de a alege trei din cele nouă date. Aflați cum se calculează, faci un mic pas pentru calcularea diferitelor probabilități.
La prima vedere, pare destul de clar de ce triunghiul dă răspunsul corect la această întrebare. Se poate, de asemenea, se pare ciudat că ar trebui să înceapă întotdeauna de la zero pentru a face să funcționeze. Pentru a vedea că toate acest lucru este perfect adevărat, vom face două observații.
În primul rând, dacă aveți un grup de obiecte, cât de multe moduri în care puteți alege obiecte de zero de la ei? Există exact o modalitate de a alege un obiect nul, și anume, pur și simplu, care să ateste că nu iei nici una dintre ele. În plus, aveți doar un singur mod de a selecta toate obiectele. Aceasta corespunde exact unităților la cele două capete ale fiecărui rând.

În al doilea rând, dacă dorim să selectați obiecte din datele, observăm că există două scenarii care se exclud reciproc: fie subiectul nostru favorit este unul dintre candidați, sau nu este. Dacă vom alege, avem, de asemenea, trebuie să selectați obiectul elementelor rămase pentru a alege exact elemente. Dacă nu vom alege subiectul, avem nevoie pentru a selecta toate articolele de la persoana vizată, rămasă după excluderea subiectului nostru preferat. Din moment ce aceasta este o oportunitate care se exclud reciproc pentru a obține numărul total de alegeri, trebuie să se stabilească numărul de opțiuni în fiecare scenariu.
Pe scurt, pentru a obține un număr de moduri de a selecta obiecte din baza de date, trebuie să se stabilească numărul de moduri de a selecta un obiect al, și numărul de moduri de a selecta obiecte din. Dar aceasta este tocmai regula plus față de triunghiul lui Pascal!
Știm deja că triunghiul este complet determinat de amplasarea unităților la laturile sale, iar regula plus. Deoarece aceste proprietăți sunt, de asemenea, aplicabile pentru a răspunde la întrebarea cu privire la numărul de obiecte de alegeri, iar triunghiul ar trebui să dea răspunsul corect aici.
Abilitatea de a face astfel de calcule este de neprețuit în multe cazuri. Prin urmare, un pic surprins de faptul că Pascal nu a fost primul. Aceste cifre au fost considerate matematicieni indieni, chinezi și iranieni la momente diferite, începând cu momentul în urmă cu mai mult de o mie de ani. Și, desigur, toată lumea va ști triunghiul Yana Hueya, 1,303 g.:
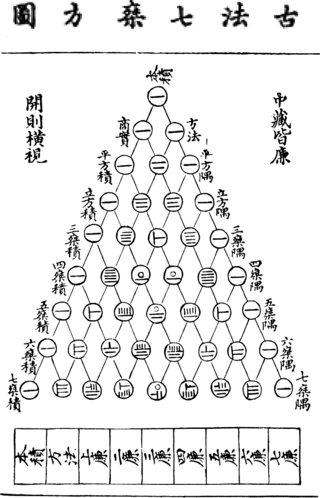
În mod ironic, chiar și fără a fi capabil să distingă numărul, puteți găsi o greșeală de tipar în acest triunghi, care este mai mult de 700 de ani! Sfat: adăugați o regulă are triunghiul lui Pascal este simetrică în raport cu linia verticală care trece prin vârful său. Dacă te uiți atent, în triunghiul Yan Hueya, această simetrie este rupt într-un singur loc.
Într-un triunghi, o mulțime de minunat. Unde sunt minunile? Unele dintre ele sunt ușor de la fața locului. Dacă adăugați la numerele din rândul i-lea al triunghiului, vei primi întotdeauna în gradul (de exemplu). Pentru noi, e destul de plictisitor.
Ceva mai interesant este faptul că, dacă adăugați până la numărul de picioare într-un triunghi pe diagonală, veți obține o secvență de numere Fibonacci. O secvență Fibonacci în sine conține multe surprize.

Să denota produsul dintre numerele din rândul i-lea al triunghiului. Deci, și așa mai departe. Numerele care sunt obținute nu par să aibă nici proprietăți miraculoase aparente. Noi Brothers a avut ideea de a vedea ce s-ar întâmpla dacă împărțiți aceste produse, calculate pentru rândurile adiacente. Mai precis, sa constatat numărul obținut prin următoarea formulă:
. Asta este, pentru fiecare rând, el a considerat fracțiunea a cărei numărător este produsul tuturor numerelor într-o linie, în picioare sub ea, și într-un rând, în picioare deasupra ei, iar numitorul - produsul tuturor numerelor din acel rând în pătrat.
Și uimitor lucru: atunci când acesta devine tot mai mult, acest raport se apropie de numărul! Amintiți-vă - acesta este un număr zecimal, cu un număr infinit de cifre, care este aproximativ egală. Se pare că atunci când capitalizarea dobânzii, numărul de modele de creștere a populației și alte situații cu o creștere exponențială. Este surprinzător faptul că acest număr poate fi un proces destul de simplu, găsit în triunghiul lui Pascal. Deci, cum știi ce să caute, este ușor de înțeles că revizuirea relațiilor într-adevăr se apropie de o creștere. După cum puteți vedea aici. de calcul este nevoie de doar un pic de algebră.
Asta este o astfel de animație drăguț Richarda Grina demonstrează rezultatul Harlan Brothers:
Există mai mult de un miracol în triunghiul, care ar trebui să știe toată lumea. Fie numărul fiecărui triunghi de culoare într-una dintre cele două culori, în funcție de faptul dacă este par sau impar. De exemplu, am putea picta chiar numere de alb, și ciudat - albastru. Dacă vom face acest lucru pentru primele 500 de linii ale unui triunghi, aici avem un model:

Este un fractal cunoscut cunoscut sub numele de Triunghiul Sierpinski! Acest lucru duce la tot felul de probleme. Numărul este par sau impar, dacă este pe diviziune prin acordarea de reziduuri sau respectiv. Ce se întâmplă când împărțim pe? Reziduurile pot fi egală sau mai mică. Ce se întâmplă dacă folosim opt culori și culoare fiecare număr, în conformitate cu restul său atunci când împărțit la opt? Pentru primele 500 de linii ale unui triunghi avem o imagine frumoasă:

Există o aplicație pic de distracție. care vă permite să vedeți ce se întâmplă dacă vom schimba numărul prin care sunt de partajare (numite module). Indicație: Atunci când utilizați aplicația, faceți clic pe simbolul mic „plus«», pentru a folosi o versiune mai detaliată a controlului. În triunghiul lui Pascal are multe alte lucruri uimitoare. Pentru început, dacă sunteți interesat de acest lucru, site-ul mathforum.org adecvat. Dar, mai mult decât, să zicem, excentric, lucruri care pot fi găsite în triunghi, există aici.
Gafelor - absurditati comise strămoși și ne-
2 VF Korneyev.:
Și cum îți place simplitatea următoarelor criterii:
numărul dacă și numai dacă un simplu, atunci când toate triunghiul lui Pascal (unitate nu contează), cu numărul liniei de numerele sunt împărțite de către acest număr.
Deoarece 9 nu este un prim deoarece 84 nu este divizibil cu 9. A 7 - simplu, deoarece toate linia a 7 este împărțit în 7.
Într-un fel prea evident, sa dovedit a fi. )
Fiecare poetomu10st.3n întreg cub = 500 x 10 Articolul 3 (n-1) + 500 x10st.3 (n-1), unde 500 x 103 (n-1) par și impar la fel de mult. Întregi începând cu 1, și numerele lor cu 0.
Murad, foarte concluzii interesante și argumente. dar nu este clar. Aș dori să aflați mai multe