Paralelismul liniei și un plan și cele două planuri - paralelismului și perpendicularitate liniei și
92 *. Prin punctul A să dețină orice linie paralelă cu planul BCD triunghi (Fig. 90, de asemenea).
Decizie. paralelă directă cu planul în cazul în care este paralelă cu orice linie dreaptă situată în planul. De aceea, prin punctul A se poate face un număr nelimitat de linii paralele cu un plan dat. De exemplu, cheltuielile (Fig. 90, b)
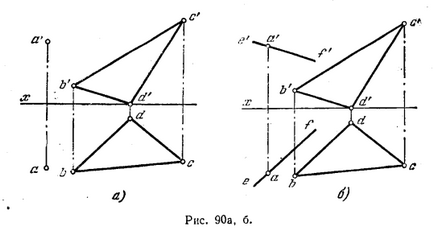
prin punctul unei „e'f directe“ B'D paralele „și printr-o linie dreaptă paralelă cu bd ef, vom obține o linie de proiecție FE paralelă cu partea laterală a BD triunghiului, și, în consecință, planul său. Selectarea liniei BD a fost arbitrară.
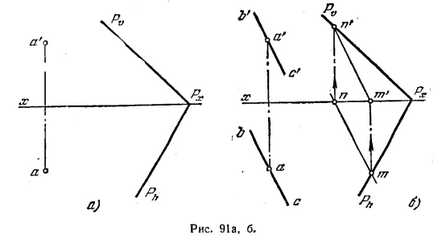
93 *. Prin punctul A să dețină orice linie paralelă cu pl. F (fig. 91 a).
Decizie. Constructul (Fig. 91.6) și m'n proiecția mn „linie dreaptă MN, situată într-un pătrat. R. Apoi, după o „ține partea din față. proiecția b a lui „m'n paralelă“,
și printr-un orizont. bc mn de proiecție paralelă. Direct soare paralel cu linia MN, și, prin urmare, planul P.
94 *. Pentru a determina dacă o linie AB este paralelă cu planul P (fig. 92 a).
Decizie. Pentru a determina dacă linia paralelă AB p.t.. P, este necesar să se încerce să efectueze în acest plan drept linie paralelă cu acest lucru. Fig. 92, al doilea front efectuat. proiecție C'D 'A'b paralele'. Construirea unui orizont. proiecție cd.
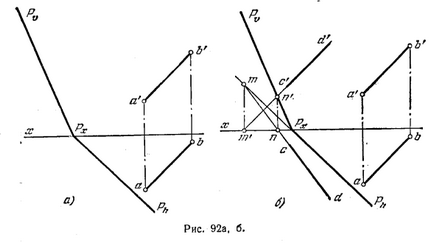
cu respectarea condiției ca CD-ul liniei trebuie să fie în pătrat. P. Deoarece proeminențele nu a fost cd construirea paralel cu ab, atunci liniile AB și CD nu sunt paralele și aceasta înseamnă că linia AB și pătrat. P nu este, de asemenea, în paralel.
Ai putea începe cu un orizont. proiecția unei linii dreaptă paralelă ab, constructul partea frontală. proiecție, care aderă la condițiile pe care această linie ar trebui să fie în pătrat. P, construit și comparat frontal. proiecție cu A'b“.
95. Determinați dacă paralel cu linia AB
a) un plan definit de liniile paralele CD și EF (Fig. 93 a)
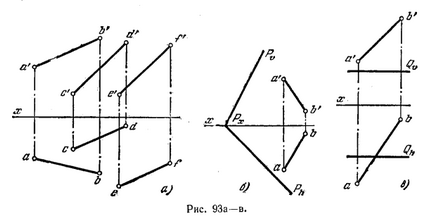
b) planul P (fig. 93 b),
a) Q plan (fig. 93 c).
96 *. Prin punctul Un plan paralel cu planul definit de punctele B, C și D (fig. 94 a).
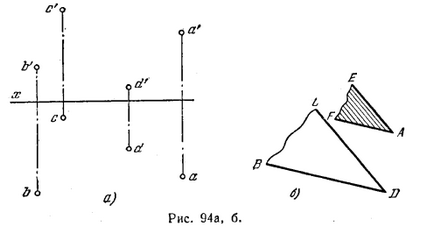
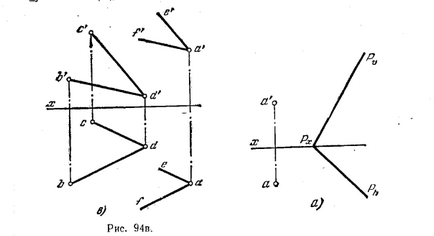
Decizie. Două avioane sunt paralele dacă cele două linii intersectate ale unuia dintre ele, respectiv, în paralel cu două linii drepte care intersectează un plan diferit (Fig. 94, b).
Pentru a construi petrece planul dorit într-un plan dat două linii drepte care se intersectează BD și CD (fig. 94, b și c). Apoi, printr-o „ține a'f“ b'd paralel „și“ e „s'd paralelă“, și printr-o paralelă BD exploatație af și CD paralel ae directă AR și AE dreaptă paralelă cu BD și CD, astfel, sunt paralele și un plan definit de ele.
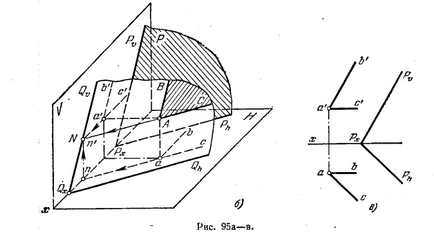
97 *. Prin punctul A (fig. 95 a) La un plan paralel mp. R.
Decizie. După cum se știe, planuri paralele orizontale paralele între ele, paralele între ele și frontal. De asemenea, urme de aceleași planuri paralele nume, respectiv, paralele între ele (fig. 95 b).
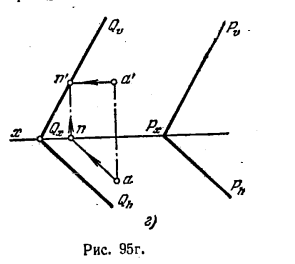
Fig. 95, și dă planul dorit prin două drepte frontale orizontale AB și AC, care printr-o „ține A'b“ paralelă Pϑ și a'c „paralelă cu axa x și prin punctul și ac conductor paralel și ab Ph paralelă cu axa x. Deoarece Trasarea Pϑ Este una dintre pătrat frontală. P, și urme Ph - una dintre contururile sale, vom obține contur paralel și frontală paralel unul și celălalt plan, adică paralel cu aceste avioane ... Fig. 95 g ilustrează structura unui plan dorit al urmelor sale Qϑ și Qh. Pentru construcția lor trasez prin punctul A plan orizontal paralel cu pista dorită și pentru a găsi față Ph. urmări N (n, n „) acestei linii orizontale. Acum, prin n „Q transportϑ || Pϑ QX găsi un punct de pe axa x și a desena o pistă paralelă Qh Ph
98. După un punct A (Figura 96.) Pentru planul paralel cu planul definit de liniile paralele CD și EF; exprimă planul dorit de două linii care se intersectează.
99. După un punct A (fig. 97) transporta PIBpp plan paralel. P; exprimă planul dorit de piesele sale.
100. După un punct A (fig. 98) transporta PIBpp plan paralel. R. Dă răspunsuri: a) exprima pl. Frontale n orizontală, b) urme.
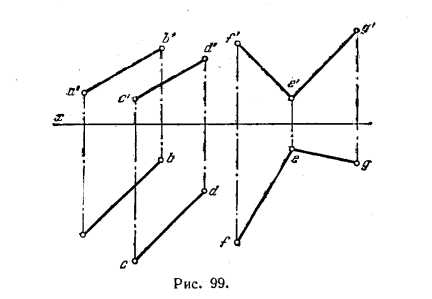
101. Pentru a determina dacă planul, dintre care unul este definit linii paralele AB și CD, precum și celelalte paralele - linii intersectându EF și EG (Figura 99.).