Program derivat

anterior ◈ următoarea

Considerăm că și compara graficul funcției și un derivat al său (figura 1)

Program derivat

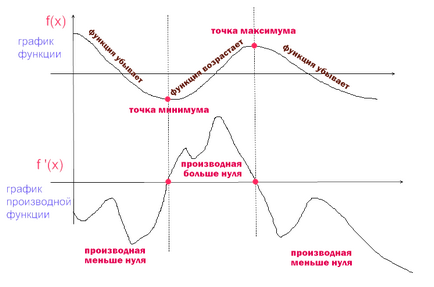
Figura 1. Un grafic al derivatului

Proprietăți Grafic derivat

  1. La intervale, în creștere derivat este pozitiv. În cazul în care derivatul de la un anumit punct într-un anumit interval este pozitiv, atunci graficul functiei in acest interval creste.
  2. La intervale de scădere a derivatului este negativ (cu semnul minus). În cazul în care derivatul de la un anumit punct într-un anumit interval este negativ, atunci graficul funcției pe intervalul scade.
  3. Derivatul la punctul x este egal cu panta tangentei la graficul funcției în acel punct.
  4. La punctele de maxim-minim al derivatului este zero. Tangenta la graficul funcției în acest punct este paralelă cu axa OX.

Graficul (Figura 2) derivat determina în ce moment pe intervalul [-3; 5] Funcția este maximizat.













Program derivat

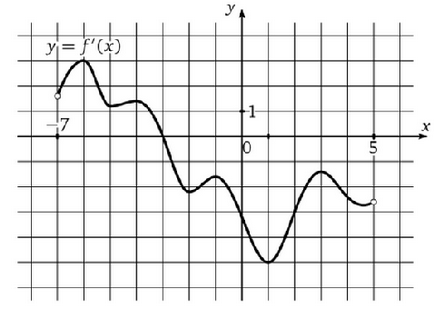
Figura 2. Diagrama derivatului

Soluție: În acest moment, în derivatul - este negativ, ceea ce înseamnă că funcția scade de la stânga la dreapta, iar cea mai mare valoare se găsește pe partea stângă la -3.

Graficul (Figura 3), pentru a determina valoarea punctelor maxime derivate pe intervalul [-11; 3].

Program derivat

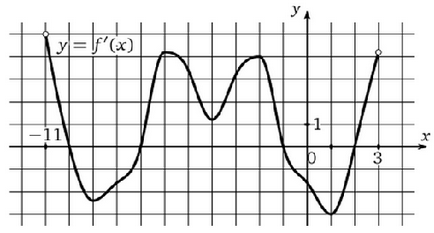
Figura 3. Derivat grafic

Soluție: puncte maxime corespund punctelor de schimbare semn al derivatului de la pozitiv la negativ. La acest decalaj de două ori funcție modifică semn de la plus la minus - la -10 și -1 punct. Prin urmare, numărul maxim de puncte - două.

Graficul (Figura 3) pentru a determina cantitatea de derivat de puncte minime ale intervalului [-11; -1].

Soluție: Punctele minime corespund punctelor de schimbare semn al derivatului de la negativ la pozitiv. În acest moment, în acest moment, doar este -7. Prin urmare, numărul minim de puncte la un interval predeterminat - una.

Graficul (Figura 3), pentru a determina valoarea punctelor extremum derivate.

Soluție: Extrema sunt puncte ca minime și maxime. Găsiți numărul de puncte la care modificările derivate semnează:

  • Punctul 10 (max)
  • Punctul -7 (minim)
  • Punctul -1 (max)
  • Punctul 2 (min)

Funcția conține 4 extremă.







anterior ◈ următoarea