Punctul de discontinuitate și tipurile lor

Determinarea punctelor de discontinuitate și speciile lor este o continuare a temei de continuitate a funcțiilor. Visual explicația (grafică) a punctelor de discontinuitate este dată, de asemenea, în contrast cu conceptul de continuitate.

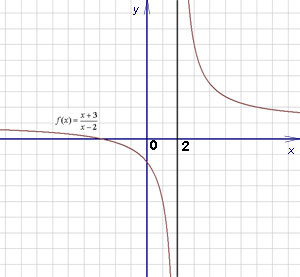
Punctele de date care nu sunt conectate între ele, sunt numite puncte de discontinuitate. Graficul unei astfel de funcții, pâraie discontinuitatea la x = 2 - - de mai jos.

O generalizare a celor de mai sus este următoarea definiție. Dacă funcția nu este continuă în punctul, atunci acesta are o discontinuitate în acest punct și punctul în sine este numit un punct de discontinuitate. Pauzele sunt primul tip și al doilea tip.

Pentru a determina tipurile de caractere () puncte Funcția de întrerupere trebuie să găsiți limitele de încredere. Prin urmare, este util pentru a deschide o fereastră nouă în lecția corespunzătoare.

Găsirea de puncte de discontinuitate poate fi ca o sarcină independentă, și o parte a unei investigații complete a funcției și reprezentări grafice.

primul tip de punct de discontinuitate: funcția de acolo ca un final (adică nu infinit egal ..) limita stânga și la sfârșitul limită dreapta, dar funcția nu este definită, sau la stânga și limitele dreapta sunt diferite (nu sunt egale).

Punctul de discontinuitate amovibil de primul tip. Stânga și în dreapta limite sunt egale. În acest caz, este posibil să se extindă definiția funcției în punctul. Extinde definiția funcției în punctul, spunând pur și simplu, înseamnă a oferi puncte de conexiune între care există un punct în care a constatat egale între ele limite stânga și dreapta. În acest sens, ar trebui să fie doar un punct în care trebuie să se găsească valoarea funcției.

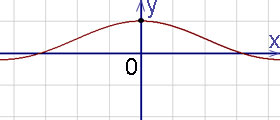
Exemplul 1. Pentru determinarea funcției punct de pauză și forma (caracterul) al punctelor de discontinuitate.

Decizie. Funcția nu este definită la punctul. Am găsit limitele stânga și dreapta ale funcției în acest moment:

Stânga și în dreapta limite sunt, prin urmare, punctul - dot discontinuitate detașabilă a primului tip.

Este posibil să se extindă definiția unei funcții:

Graficul punctului de break cu - sub exemplu.

Pentru calcularea limitelor de auto-control, puteți utiliza limitele calculator online.

punctul inamovibil (final) al primului tip de discontinuitate. Există limite stânga și la dreapta, dar ele sunt diferite (nu sunt egale). Este imposibil să se extindă definiția funcției. Limita diferență se numește saltul.

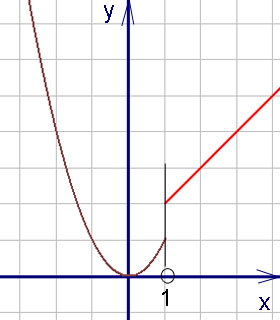
Exemplul 2. Determinarea funcției breakpoint și forma (caracter) punctelor de discontinuitate a funcției

Decizie. Este evident că schimbările în exprimarea punctului funcției. Găsiți limitele stânga și dreapta ale funcției în acest moment:

Stânga și în dreapta limite nu sunt egale, prin urmare, punctul - punctul inamovibili (final) al primului tip de discontinuitate. Graficul punctului de break cu - sub exemplu.

Pentru calcularea limitelor de auto-control, puteți utiliza limitele calculator online.

Găsirea de puncte de discontinuitate poate fi ca o sarcină independentă, și o parte a unei investigații complete a funcției și reprezentări grafice.

al doilea fel de punct de discontinuitate: punctul în care cel puțin una dintre limitele (stânga sau dreapta) - infinit (egal cu infinit).

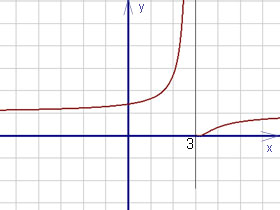
Exemplul 3. Determinarea funcției breakpoint și forma (caracter) punctelor de discontinuitate a funcției

Decizie. De la nivelul de expresie văzută la e, că punctul nu este definit. Găsiți limitele stânga și dreapta ale funcției în acest moment:

Una dintre limitele este infinit, astfel încât punctul - un punct de discontinuitate al doilea tip. Graficul punctului de break cu - sub exemplu.

Pentru calcularea limitelor de auto-control, puteți utiliza limitele calculator online.

Găsirea de puncte de discontinuitate poate fi ca o sarcină independentă, și o parte a unei investigații complete a funcției și reprezentări grafice.

Și câteva exemple.

Exemplul 4. Determinarea funcției breakpoint și forma (caracter) punctelor de discontinuitate a funcției

Decizie. De la nivelul expresiei la 2 că punctul nu este definit. Găsiți limitele stânga și dreapta ale funcției în acest moment:

Limitele nu sunt egale și finit, astfel încât punctul - punctul de ruptură ireparabilă a primului tip. Graficul punctului de break cu - sub exemplu.

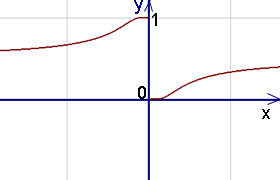
Pentru calcularea limitelor de auto-control, puteți utiliza limitele calculator online.

Exemplul 5. Determinarea funcției breakpoint și forma (caracter) punctelor de discontinuitate a funcției

Decizie. Este clar că punctul nu este definit. Găsiți limitele stânga și dreapta ale funcției în acest moment:

Ambele limite sunt nelimitate, astfel încât punctul de - al doilea tip de punctul de discontinuitate. Graficul punctului de break cu - sub exemplu.

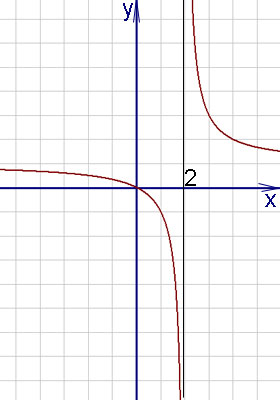
Pentru calcularea limitelor de auto-control, puteți utiliza limitele calculator online.