Radian și gradul de măsură a unghiului

Aici considerăm problema Proc32 - Proc33 de Taskbook Abrahamyan: descrierea funcțiilor de conversie de la unghiurile de grade la radiani și vice-versa.

Deci, ce este măsura radiani un unghi? Să considerăm un cerc cu raza R centrată la O. Deoarece cercul este împărțit în 360 de grade, iar lungimea circumferențiară este 2πR, apoi 1 grad de lungime de arc au egal 2πR / 360 = πR / 180. Apoi unghiul α grade corespunde lungimii arcului L = πRα / 180.

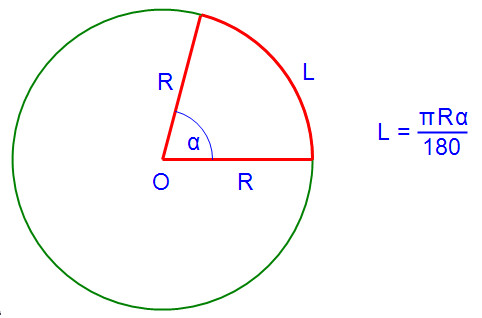
În acest sens, situația este foarte interesant atunci când lungimea arcului L este egală cu raza cercului R. Ce cu unghi arc? Reamintind formula anterioară pentru calcularea lungimii arcului, avem: πRα / 180 = R, unde πα / 180 = 1, și obținem α = 180 / π.

Astfel, în cazul în care lungimea arcului este egală cu raza cercului, unghiul corespunzător este de 180 / π. Acest unghi este numit radian (Rad):

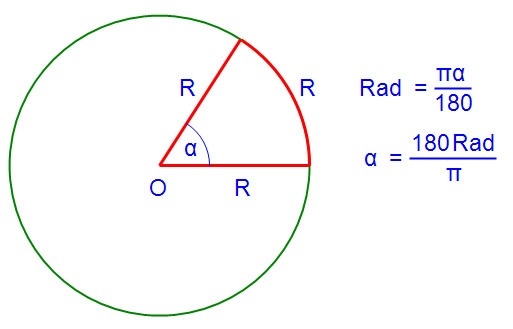
1 Rad = 180 / π grade.

tt radiani = 180 ° și 1 ° = tt / 180 radiani.

măsură radian unghiului - aceasta este o astfel de măsură de unghiul la care a primit 1 unghi Rad de arc, egală cu raza arcului. Deoarece 1 radian corespunde lungimii arcului egală cu raza, aceasta implică următoarea concluzie:

Amploarea măsurii radian a unghiului este egal cu raportul dintre arc și raza acestui cerc.

De exemplu, în cazul în care lungimea arcului este egală cu 1.5R, măsura radian unghiului arcului este egal cu 1,5; Dacă lungimea arcului este egală cu 0.25R, măsura radian egală cu 0,25; 2PR lungimea arcului (întreaga circumferință) măsură radian este egală cu 2tt etc. In general, lungimea arcului L unghiul în radiani este egal cu L / R, unde R - raza.

Radian - este un mod foarte convenabil de măsurare a unghiurilor, pentru că în loc de unghiuri în sine, putem opera cu rapoarte de lungimi de arce și raze. În matematică mai mare decât măsură radian utilizat în toate funcțiile trigonometrice.

Proc32. Descrie funcția DegToRad (D) din material care returnează valoarea unghiului în radiani, în cazul în care magnitudinea sa este dat în grade D (D - un număr real, 0 ≤ D <360). Воспользоваться следующим соотношением: 180° = π радианов. В качестве значения π использовать 3.14. С помощью функции DegToRad перевести из градусов в радианы пять данных углов.