triunghi isoscel
scop
• Pentru a familiariza studenții cu un triunghi isoscel;
• Continuă să formeze abilități de construcție triunghiuri unghiulare;
• Creșterea cunoștințelor elevilor despre proprietățile triunghiuri isoscele;
• Fixati cunoștințele teoretice pentru a rezolva problemele.
obiectivele lecției
• Pentru a fi în măsură să formuleze, dovedi și de a folosi teoreme privind proprietățile unui triunghi isoscel în procesul de rezolvare a problemelor;
• Continuarea dezvoltării percepției conștiente de material educațional, gândirea logică, abilități de auto-evaluare de auto-monitorizare și;
• Apelați interesul cognitiv la lecțiile de matematică;
• Educați activitate, curiozitate și organizare.
plan de lecție
1. Concepte generale și definiții ale triunghiului isoscel.
2. Proprietăți ale unui triunghi isoscel.
3. Semne ale unui triunghi isoscel.
4. Întrebări și sarcini.
triunghi isoscel
triunghi isoscel - un triunghi având două laturi egale, care sunt numite laturile unui triunghi isoscel, iar partidul său a treia numită bază.
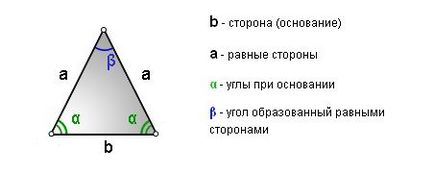
Punctul culminant al acestei cifre este cea care se află în fața bazei sale.
Unghiul, care se află vizavi de bază se numește unghiul la vârful acestui triunghi, iar celelalte două sunt numite unghiuri de colt la baza unui triunghi isoscel.
Tipuri de triunghiuri isoscele
triunghi isoscel, precum și alte figuri pot avea diferite puncte de vedere. Printre isoscel unghi-acute triunghiuri întâlni, dreptunghiulare, obtuz și echilateral.
• triunghi acută are toate unghiurile acute.
• Y triunghi vârfurile unui unghi drept și unghiurile acute situate la baza.
• obtuz are un unghi la vârf obtuz, iar la unghiurile de bază sunt acute.
• Do echilateral toate unghiurile și laturile sale sunt egale.
Proprietățile unui triunghi isoscel
• unghiuri opuse în raport cu laturile egale ale unui triunghi isoscel sunt egale;
• Bisectors, medians și înălțime, realizate din unghiuri opuse laturile egale ale triunghiului sunt egale.
• bisectoare, mediană și înălțime, regizat și a efectuat la baza triunghiului coincide cu unul de altul.
• centre ale cercurilor inscriptionare circumscrise se află pe altitudinea, bisectoarea si mediana (acestea corespund) efectuate la sol.
• Opoziția față de laturile egale de un triunghi isoscel unghiuri, întotdeauna ascuțite.
Aceste proprietăți ale unui triunghi isoscel sunt utilizate în rezolvarea problemelor.
teme pentru acasă
1. Dă-o definiție a unui triunghi isoscel.
2. Care este Particularitatea acestui triunghi?
3. Care este diferența dintr-un triunghi isoscel dreptunghiulare?
4. Proprietăți Ce cunoscute ale unui triunghi isoscel.
5. Ce crezi, este posibil, în practică, pentru a verifica egalitatea unghiurilor la baza și cum se face?
Și acum să aibă un pic de test și de a afla cum vă apucați un material nou.
Ascultați cu atenție și să răspundă la întrebări dacă această afirmație este adevărată, că:
1. Triunghiul poate fi considerat ca un isoscel în cazul în care are două părți sunt egale?
2. bisectoare se numește un segment care leagă vârful triunghiului cu punctul de mijloc pe partea opusă?
3. bisectoarea unui segment de linie care împarte unghiul care leagă partea de sus partea opusă a punctului în jumătate?
Sfaturi pentru rezolvarea problemelor unui triunghi echilateral:
1. Pentru a defini perimetrul unei lungime laterală triunghi isoscel suficient pentru a se înmulțește cu 2 și se adaugă această lucrare cu baze triunghiulare în lungime.
2. În cazul în care problema cunoscută perimetrul și lungimea bazelor triunghi isoscel, apoi pentru a găsi lungimea laturii de baze este suficient pentru a ține departe de lungimea perimetrului și a diferenței constatate împărțit la 2.
3. Și, în scopul de a găsi lungimea bazele unui triunghi isoscel, și cunoscând perimetrul și lungimea laturii, este necesar doar să se multiplice partea de două și scade acest produs din perimetrul nostru al triunghiului.
1. Printre triunghiuri din figura definesc un plus, și explicați alegerea ta:
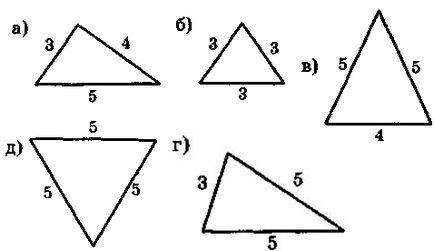
2. Se determină triunghiurilor descrise în figura sunt isoscel, numele de bază și părțile acestora, precum și calcula perimetrul lor.
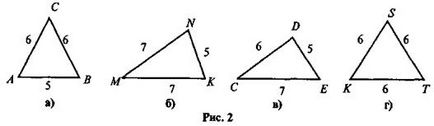
3. Perimetrul unui triunghi isoscel este de 21 cm. Gaseste laturile acestui triunghi, în cazul în care una dintre ele este mai mare de 3 cm. Câte soluții pot avea această sarcină?
4. Este cunoscut faptul că, dacă o parte laterală și un unghi opus bazat pe una de triunghi isoscel este egală cu latura și colțul celălalt, aceste triunghiuri sunt egale. Dovedește această declarație.
6. În cazul în care părțile la un triunghi isoscel sunt egale cu 4 m și 5 m, ceea ce este perimetrul său? Cât de multe soluții pot avea această problemă?
7. Dacă unul dintre colțurile unui triunghi isoscel este egală cu 91 de grade, care sunt egale cu unghiurile rămase?
fapte interesante
Vreunul dintre voi stiti ce triunghiul lui Pascal? Sarcina de a construi triunghiul lui Pascal este adesea solicitat să verifice abilitățile de programare elementare. În general, triunghiul lui Pascal se referă la combinatorică și teoria probabilității. Deci, ce fel de triunghi?
triunghiul lui Pascal - un triunghi aritmetică fără sfârșit sau o masă în formă de triunghi, care este format cu ajutorul coeficienților binomiali. În cuvinte simple, în partea de sus triunghi și părțile laterale sunt una, iar el este umplut cu suma a două numere, care sunt situate mai sus. Ori acest triunghi este fără sfârșit, dar dacă conturul ei, atunci vom obține un triunghi isoscel cu rânduri simetrice în raport cu axa sa verticală.
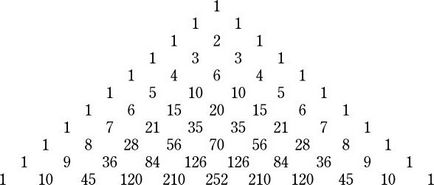
triunghiuri isoscel salvat din cele mai vechi timpuri grecii și egiptenii în determinarea distanțelor și înălțimile. De exemplu, grecii antici au fost determinate cu ajutorul distanței distanța până la o navă pe mare. Și egiptenii antici au măsurat înălțimea de piramide din cauza lungimii lor de umbre turnate, ca este un triunghi isoscel.
Din cele mai vechi timpuri, oamenii au apreciat deja frumusețea și caracterul practic al acestei cifre, ca forma de triunghiuri ne înconjoară peste tot. Mutarea prin diferite sate, putem vedea acoperișurile caselor și a altor clădiri care ne amintesc de un triunghi echilateral, merge la magazin, am găsit sacii cu alimente și sucuri de formă triunghiulară și chiar unele chipuri umane sunt în formă triunghiulară. Această cifră este atât de popular încât să poată fi găsite la fiecare pas.