Viteza și accelerația punctului

Viteza și accelerația

punct de viteză

Într-o mișcare a corpului articol anterior sau un punct definit ca o modificare a poziției în spațiu a lungul timpului. Pentru a descrie mai complet aspectele calitative și cantitative ale mișcării introduse concepte de viteză și de accelerație.

Viteza de deplasare - o mișcare de măsură cinematică a unui punct, care caracterizează rata de schimbare a poziției sale în spațiu.
Viteza este o mărime vectorială, T. E. Aceasta se caracterizează nu numai modul (component scalare), dar și direcția în spațiu.

După cum se știe din fizică, viteza uniformă de mișcare poate fi determinată lungimea căii traversată pe unitatea de timp: v = s / t = const (se presupune că originea și modul în care, în același timp).
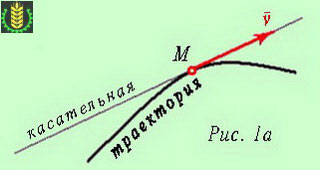
În viteza de deplasare liniară și modulul constant și direcția, și coincide cu traiectoria vectorului.

Viteza Unitate în sistemul SI este definită de lungimea / timpul t. E. M / s.

Evident, la punctul de viteza de mișcare curbilinie va fluctua în direcția.
Pentru a stabili direcția vectorului de viteză în fiecare moment în mișcare curbilinie, împărțiți traiectoria în secțiuni infinitezimale pistă care pot fi considerate (ca rezultat al micimea lor) rectiliniu. Apoi, la fiecare loc vzg viteză condiționată astfel de mișcare rectilinie este direcționat de-a lungul corzii, iar coarda, la rândul său, scade la lungimea arcului infinit (Δs tinde la zero), va coincide cu tangenta la arc.
Din aceasta rezultă că atunci când vectorul viteză de mișcare curbilinie, la fiecare moment coincide cu tangenta la traiectoria (Fig. 1a). mișcare rectilinie poate fi reprezentat ca un caz particular de mișcare curbată de-a lungul arcului a cărui rază se apropie de infinit (traiectoria coincide cu tangenta).

La mișcare neuniformă a unui punct modulul vitezei sale variază în funcție de timp.
Imaginați-vă un punct, a cărui mișcare este stabilită într-un mod natural prin ecuația s = f (t).

În cazul în care într-o perioadă scurtă de timp a trecut la punctul At Δs. apoi viteza medie este egală cu:

Viteza medie nu reprezintă adevărata viteza la un moment dat în timp (viteza reală este, de asemenea, numit instantanee). Evident, mai mic intervalul de timp pentru care se determină viteza medie, cat este mai aproape de valoarea vitezei instantanee.

Rata Adevărat (instantanee) este limita la care viteza medie tinde în timpul At, tinde la zero:

v = lim t → Vav la 0 sau v = lim (Δs / At) = ds / dt.

Astfel, o valoare numerică egală cu adevărat viteza v = ds / dt.
Adevărata viteza (instantanee) de mișcare în orice punct este prima derivată a coordonatelor (m E. Distanța de la originea mișcării.) În timp.

Când se duce la zero At, Ds tinde la zero, și, după cum am văzut, vectorul viteză este direcționat de-a lungul tangentei (t. E. La fel ca și adevărata viteză vector v). Din aceasta rezultă că limita de viteza vectorului vzg condiționată. egal cu raportul limita punctelor vectorului de mișcare la un interval de timp infinitezimal este egal cu adevăratele puncte vector de viteză.

Punct accelerare mișcare rectilinie

În general, mișcarea punctelor cu o viteză care variază în timp numit accelerat, in timp avand in vedere accelerarea provocând reducerea vitezei, negativ. Uneori mișcarea, în care rata scade cu timpul, numit întârziat.

Accelerarea are o măsură cinematică a ratei de schimbare a punctului în timp. Cu alte cuvinte - accelerația - este rata de schimbare de viteză.
Viteza, accelerația este o mărime vectorială, T. E. Nu numai caracterizate printr-un modul, dar și direcția în spațiu.

In vectorul vitezei de mișcare rectilinie coincide întotdeauna cu traiectoria și astfel încât rata vector de schimbare coincide cu traiectoria.

Desigur, în fizică este cunoscut, că accelerația este variația vitezei de circulație pe unitatea de timp. În cazul în care într-o perioadă scurtă de timp, viteza sa schimbat punctul de la At Av. accelerația medie pe o anumită perioadă de timp a fost: ACP = Av / At.

accelerație medie nu oferă o idee despre adevărata valoare a ratei de schimbare la un moment dat. Este evident că mai mic intervalul de timp considerat în timpul căreia a avut loc modificarea vitezei, mai aproape de valoarea accelerației este de adevărat (instantanee).






Din această definiție: true (instantanee) de accelerație este limita spre care accelerația medie în timpul At. tinde la zero:

și când Asr = lim t → 0 sau lim Av / = At ​​dv / dt.

Dat fiind faptul că v = ds / dt. Obținem: a = dv / dt = d 2 s / dt 2.

Adevărata accelerare în mișcare rectilinie este egal cu primul derivat sau derivata a doua a coordonatelor vitezei (distanța de la originea mișcării) în timp.

Unitatea de accelerare - metru împărțit la secundă la pătrat (m / s 2).

Puncte de accelerare în mișcare curbilinie

Atunci când se deplasează de-a lungul unui traseu curbat schimbari punct vitezei de direcție, adică. Vectorul viteză F este variabilă.

Imaginați-vă un punct M, care în timp At. se deplasează de-a lungul unui traseu curbat, sa mutat la poziția M1 (fig. 1).

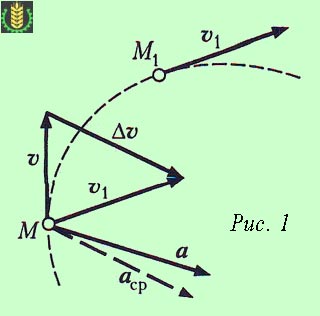
increment vector (schimbare) notată viteză Av. apoi: = v1 Av - v.

Pentru a găsi vectorul v1 transfera Av vector în punctul M și construi triunghiul de viteză. Noi definim vectorul de accelerație medie:

Asr vector paralel cu vectorul Av. deoarece cantitatea vector prin împărțirea direcția vectorului scalare nu se schimbă.
Vectorul adevărata accelerație este o limită la care raportul vitezei tinde vectorul increment la intervalul de timp corespunzător, atunci când acesta din urmă tinde la zero:

a = lim Av / t → la At 0.

O astfel de limită numit un derivat al vectorului.
Astfel, adevărata accelerare a punctului în vectorul de mișcare curbiliniu este egal cu derivata vitezei.

Figura 1 arată că vectorul accelerație în mișcare curbiliniu este întotdeauna îndreptată spre concavitatea căii.

Deoarece vectorul derivat calcula direct nu putem, atunci accelerația în mișcare curbiliniu va defini metode indirecte. De exemplu, în cazul în care mișcarea unui punct stabilit într-un mod natural, apoi aplicați teorema proiecții ale tangenta accelerației și normale. Pentru a înțelege esența acestei teoreme, este necesar să se ia în considerare conceptul de linii de curbură a curbelor.

Conceptul de curbura curbelor

Să considerăm traiectoria curbată a punctului M (fig. 2a).
Unghiul Δφ între tangentele la curbă, la două puncte vecine se numește unghiul de adiacenta.

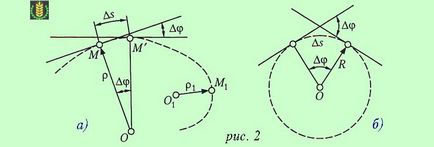
Curbura curbei la acest punct este raportul contiguitate unghiul limită Δφ corespunzând lungimii arcului Δs, atunci când acesta din urmă tinde către zero.
Notăm curbura literei k. atunci:

k = lim Δφ / Δs când Δs → 0.

Să considerăm un cerc de rază R (a se vedea. Figura 2b).
Deoarece Δs = RΔφ. atunci:

k = lim Δφ / Δs = lim Δφ / RΔs = 1 / R (când Δs → 0).

În consecință, curbura unui cerc, la toate punctele identice și egale cu k = 1 / R.

Pentru fiecare punct al curbei se poate alege un cerc a cărui curbură egală cu curbura curbei la acest punct. Raza care p a unui astfel de cerc se numește raza de curbură a curbei la un anumit punct și centrul acestui cerc - centrul de curbură.

Astfel, curbura curbei în acest moment este inversul razei de curbură în acest punct.

Evident, curbura unei linii drepte este zero, iar din raza de curbură a unei astfel de linii este egal cu infinit.

O teoremă pe proiecții ale accelerației pe tangenta și normală

Proiecția accelerației pe tangenta la traiectoria se numește tangentă accelerația (tangențial), și accelerarea protuberanța normală la tangenta - accelerația normală.

Teorema: accelerația normală este egală cu pătratul vitezei împărțită la raza de curbură a căii în acest moment; accelerația tangențială - prima derivată a vitezei în raport cu timpul.

Dovada se bazează pe construcții geometrice, ținând cont de dependențele menționate anterior deplasării, vitezei și accelerației în funcție de timp. În această lucrare, dovada nu este dat; dacă este necesar, este posibil să se ia în considerare alte surse de informații.

Deci, pe baza teoremei de pe accelerație, putem scrie:

ap = v 2 / ρ; aτ = dv / dt.

Analizând formula tangentei și accelerația normală, putem concluziona că accelerația tangențială caracterizează viteza de schimbare este doar în valoare absolută, și normal - numai într-o direcție.

Cunoscând valoarea accelerației normală și tangențială, puteți calcula accelerația totală a unui punct, folosind teorema lui Pitagora:

Direcția de accelerare: cos (aτ, a) = aτ / a.

Adesea accelerația tangențială și normală nu sunt considerați ca proiectii, ci ca elemente de accelerație maximă, r. E. Cum cantități vectoriale.

vector accelerație normală este întotdeauna îndreptată spre centrul de curbură, astfel încât accelerația este uneori numit centripetă.

Tipuri de puncte de circulație, în funcție de accelerația

Formula Analyzing accelerația tangențială și normale sunt următoarele tipuri de puncte de circulație:

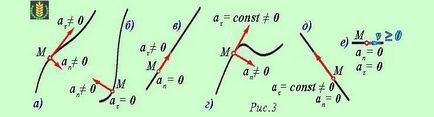
ap = v 2 / ρ ≠ 0; aτ = dv / dt ≠ 0. - curbiliniu neregulată (Figura 3a).

ap = v 2 / ρ ≠ 0; aτ = dv / dt = 0. - curbiliniu uniformă (Figura 3b.);

ap = v 2 / ρ = 0; aτ = dv / dt ≠ 0. - rectiliniu inegale (Figura 3b.);

aτ = dv / dt = const ≠ 0; ap = v 2 / ρ ≠ 0. - ravnoperemennoe curbiliniu (Figura 3a.);

aτ = dv / dt = const ≠ 0, ap = v 2 / ρ = 0. - ravnoperemennoe rectiliniu (Figura 3d.);

ap = v 2 / ρ = 0; aτ = dv / dt = 0. - liniară uniformă (mișcare fără accelerație) (Figura 3e.).

Teoreme privind proiecția vitezei și accelerației pe axa de coordonate

Dacă mișcarea punctelor de coordonate metodei definite, distanța (deplasare), viteza și accelerația în timpul intervalului de timp At poate fi găsit folosind proiecția acestor valori pe axa de coordonate. Evident, orice creștere a coordonatelor atunci când se apropie de zero, de asemenea At tinde spre zero, iar limita sporului poate fi determinată de relațiile diferențiale teoremelor stabilite asupra proiecțiilor vitezei și accelerației:

Teorema: proiecția vitezei pe axa de coordonate este prima derivată a timpului corespunzător de coordonate:

Teorema: o proiecție pe axa de coordonate a accelerației este derivata a doua a coordonatei corespunzătoare timpului:

ax = d 2 x / 2 ay = At ​​d 2 y / 2 az = At ​​d 2 z / 2 At.

Cunoscând viteza sau accelerația proiecției pe axele de coordonate, este posibil să se determine mărimea și direcția vectorului de oricare dintre aceste valori folosind teorema lui Pitagora și relațiile trigonometrice.