charting Mathcad

suprafață ( „grafic de suprafață“);

vector ( "câmp vectorial").

La selectarea construirea unui grafic bidimensional în axele de coordonate X, Y pe șablonul foii de lucru este creat (figura 1. 19) cu câmpuri substituenți pentru a specifica datele afișate pe axele abscisei și ordonatei (nume de argumente și funcții sau expresii la acestea, precum și intervale schimbarea valorilor). Substituent în mijlocul axelor pentru variabile sau expresie afișată pe această axă.

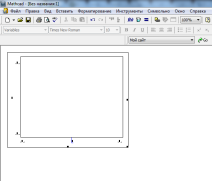
Fig.1. 19 șablon Blank bidimensionale grafică.

Agregate pentru valorile limită apar după argument și / sau funcția de intrare. Valorile limită ale axelor sunt selectate automat, în funcție de intervalul de valori de schimbare, dar ele pot fi stabilite printr-un clic pe câmpurile, agregate corespunzătoare și modificarea valorilor în ele.

Fig.1. 20 prezintă parametrii șablon completate, intervalele valorice ale axelor sunt definite manual. Rețineți că aceste valori sunt vizibile numai în modul grafic de editare (prezența cursorului unghiulare în figuri arată că blocul graficului curent selectat).

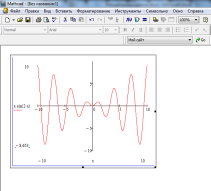
Fig.1. 20 bidimensională grafic.

Axa abscisa reprezintă o variabilă care specifică valori la limită (ca în Fig.1. 20) pentru ea. Umpluturile in ordonata plasate de obicei, funcția sau vectori de expresie.

Într-o zonă grafică vă puteți construi câteva grafice. În acest scop, este necesar ca la axa respective enumera câteva expresii separate prin virgulă (Fig.1. 21).

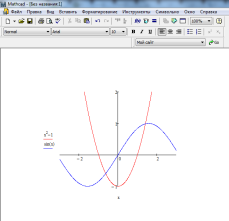
Fig.1. 21. Construcția celor două grafice în același sistem de coordonate.

Diferite curbe sunt prezentate în culori diferite, precum și pentru a specifica elementele de format grafic trebuie să faceți dublu clic pe zona graficului. Pentru a controla afișarea liniilor trasate servește Urme tab (urme) din caseta de dialog (Fig. 1. 22). Formatul actual al fiecărei linii este afișată în listă, precum și o listă a elementelor de control, vă permit să modificați formatul. Câmp Tag legendă (Legenda Label) Descriere definește o linie care este afișată numai atunci când steagul este resetat la „Ascunde descrierea“ (ascunde Legenda). Listă Simbol (simbol) vă permite să selectați pentru markeri specifică tipul de linie, o listă de culori (Color) linie de listă de puncte individuale (linie) - culoarea. Tip de listă (Tour) specifică o metodă de comunicare de puncte selectate și o listă de dimensiune (lățime) - lățimea liniei.

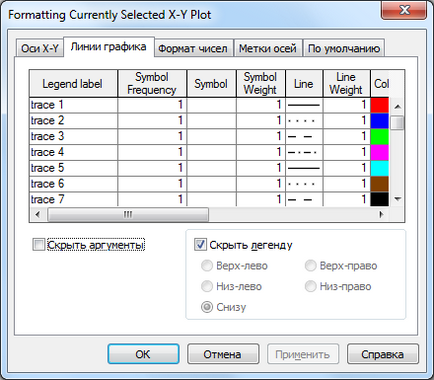
Fig.1. 22. Sarcina de programare tipuri de linii.

In mod similar construite și formatate grafic în coordonate polare, și ar trebui să stabilească valori de matrice prestabilite ale coordonatelor punctelor pentru alte tipuri de grafice.

Recomandări pentru utilizarea funcției root.

Cu cât este mai precisă selectat apropierea inițială a rădăcinii, rădăcina va converge rapid.

Pentru a schimba precizia cu care căutări funcția rădăcină pentru rădăcina de necesitatea de a modifica valoarea unui TOL variabile de sistem. În cazul în care crește valoare TOL, funcția rădăcină converge mai repede, dar răspunsul va fi mai puțin precise. Dacă TOL este redusă, funcția rădăcină converge încet, dar răspunsul va fi mai precisă. TOL Pentru a schimba valoarea unui anumit punct al documentului de lucru, definirea formei Tol = 0,01. TOL Pentru a modifica valoarea pentru întreaga documentului de lucru, faceți clic pe InstrumentyOptsii foaie de lucru ... Vstroennye convergență peremennyeDopusk (TOL).

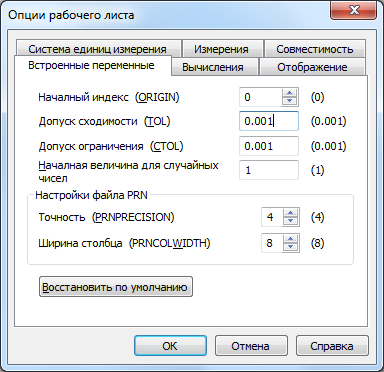
Fig.1. 23. Stabilirea exactității calculelor.

Dacă cele două rădăcini sunt dispuse aproape unul de altul, scad TOL, pentru a le distinge.

Dacă funcția f (x) are un pas redus de aproximativ rădăcină dorită, funcția root (f (x), x) poate converg spre r valoare. îndepărtat de la rădăcină destul de departe. În astfel de cazuri, în scopul de a găsi o valoare mai exactă necesară pentru a reduce valoarea rădăcină TOL.

Pentru expresia f (x) cu cunoscute constatare rădăcină și rădăcini suplimentare f (x) este echivalentă cu găsirea rădăcinilor h (x) = f (x) / (x - a). O astfel de metodă este utilă pentru găsirea rădăcinilor dispuse aproape unul de altul. Pur și simplu căutați rădăcina h expresie (x), decât să încerce să găsească o altă rădăcină a ecuației f (x) = 0, prin alegerea diferitelor aproximările inițiale.