Cum de a rezolva problemele c2 examen de matematica - sfaturi de tutore

Cum de a rezolva problema C2 examenul la matematică - sfaturi tutoror

Cum de a învăța cum să rezolve problema examenului C2 la matematică? Această problemă apare în ajunul examinării viitorilor absolvenți sunt din ce în ce. Ca un tutore în matematică, pentru o lungă perioadă de timp angajat în pregătirea studenților pentru a trece examenul, voi dezvălui astăzi mai multe secrete legate. Există trei metode de bază pentru rezolvarea problemelor de examen C2 la matematică. Să-i numim „metodă de construcție“, „metoda vector“ și „metoda volumului.“ Fiecare dintre ele este util într-un caz particular, deci este mai bine să știe și să fie capabil să utilizeze toate cele trei (Consiliul Matematician).

Cel mai versatil este „metoda de construire“, acesta poate fi folosit pentru a rezolva aproape orice problemă în geometria solidă de cele oferite în examen în variantele de matematică. Cu toate acestea, nu este întotdeauna practic în termeni de timp și costuri de calcul. În acest caz, în ajutorul celorlalte două metode. Dar, mai întâi lucrurile primele.

Deci, ce aveți nevoie pentru a rezolva problema folosind C2 „metodă de construcție“. O condiție necesară (dar cu siguranță nu suficientă) este cunoașterea și înțelegerea teoremele de bază ale geometriei solide, legate de dispunerea reciprocă a liniilor și avioane în spațiu perfectă. Acestea vor fi necesare pentru a dovedi că în mod necesar să însoțească soluția la aproape orice problemă C2, fără de care ar putea fi pierdut unele puncte pentru această sarcină în examen. Aici ca și în bază de referință al acestor teoreme.

1. Semnul de paralelism al liniei drepte și plane

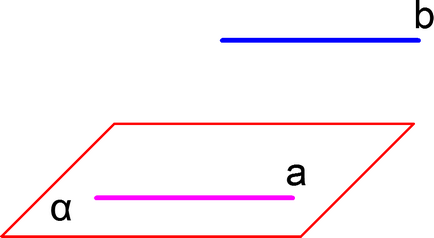
Semn de paralelism al liniei drepte și plane

În cazul în care linia nu se află în planul paralel cu oricare linie dreaptă situată în planul, este paralelă cu acest plan. Figura linie nu se află într-un plan, dar este paralel cu o linie dreaptă, situată într-un plan paralel cu planul liniei, astfel,

2. Simptom de planuri paralele

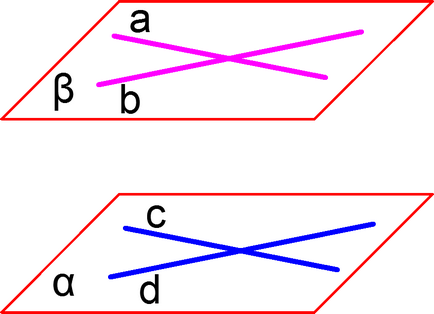
Simptom de planuri paralele

În cazul în care două linii drepte care se intersectează care aparțin aceluiași plan, sunt paralele cu două drepturi aparținând un alt avion, atunci aceste planuri sunt paralele. Cifra dreaptă și deține avionul și se intersectează, în mod direct și deținute avionul și se intersectează, în afară de o paralelă directă cu linia, și linia dreaptă paralelă cu linia, astfel încât planul și paralel.

3. Simptom linie perpendiculară și planul

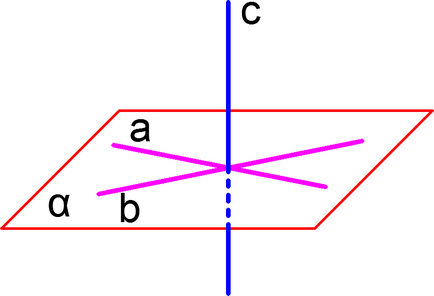
Simptom linie perpendiculară și un avion

Dacă o linie dreaptă perpendiculară pe două linii intersectate care aparțin unui anumit plan, o astfel de linie dreaptă este perpendiculară pe acest plan. Cifra dreaptă și se află într-un plan și se intersectează perpendicular și drept înainte și, prin urmare, drept o perpendiculară directă pe planul

4. Teorema pe trei perpendicularele

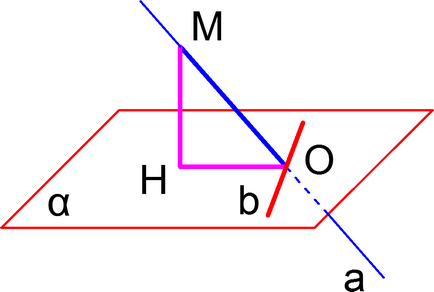
Teorema pe trei perpendicularele

Direct. O linie dreaptă situată în planul perpendicular și proiecție oblică pe acest plan, este perpendicular pe cel mai înclinat.

Contact. O linie dreaptă situată într-un plan înclinat și perpendicular, și perpendicular pe această proiecție înclinată pe acest plan.

Figura plan înclinat intersectează linia punct din punct aparținând perpendiculară pe planul punctului de bază servește ca un segment perpendicular - proiecția pe un plan înclinat în planul perpendicular pe linia dreaptă perpendiculară pe mijlocul de proiecție și conversa mai înclinată este de asemenea adevărat.

5. planuri perpendiculare caracteristice

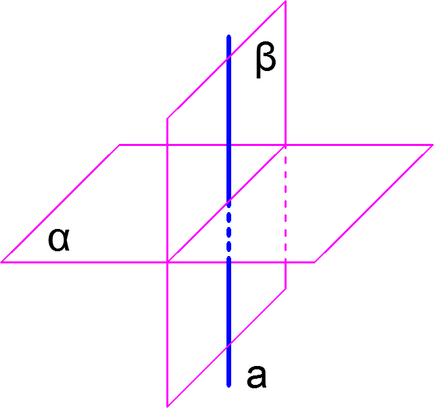
Simptom perpendicular plane

În cazul în care avionul trece prin linia dreaptă care este perpendicular pe un alt plan, aceste planuri sunt perpendiculare. Figura plane drepte perpendicular pe planul trece prin linia astfel plan perpendicular pe planul

În plus față de cunoaștere a acestor teoreme, veți avea nevoie de capacitatea de a construi sarcinile necesare unghiurile și distanțele. Într-o referire amintesc ce se înțelege prin distanțele și unghiurile dintre liniile drepte și avioane în geometrie solidă.

Coordonata X a punctului B - este lungimea AM intervalul este egal cu 0,5. Într-adevăr, BM - înălțime, realizată într-un triunghi echilateral, de aceea este atât mediana. Acesta este AM = MC = 0,5. Un desen, deci nu spun, dar asta e cum sa întâmplat. Geometrie - știința în mod corespunzător rezolva problemele pe cifrele greșite :-). Coordonata Y punctul B - este lungimea segmentului BM, care este teorema lui Pitagora pentru triunghiul din dreapta BMC. Coordonata Z a punctului B este egal cu 0, deoarece punctul este în planul XOY.