Exemple de rezolvare a problemelor - studopediya
Exemplul 1. Se determină potențialul de ionizare și primul potențial atom de hidrogen de excitație.
Ionizare potențial Ui numit cea mai mică diferență de potențial care trebuie să treacă într-un câmp de electroni de accelerare la coliziunea cu atomul de neexcitat ioniza-l. De lucru pentru a îndepărta electronul din atomul Ai este intensitatea câmpului electric care accelerează electron, EUI. Prin urmare, Ai = EUI.
Având în vedere natura cuantică a absorbției de energie de către atomul, putem spune că lucrarea de ionizare Ai este cuantumul hv energiei. atom de hidrogen absorbit la trecerea unui electron din prima orbita Bohr orbita la infinit. Apoi, aplicarea unei serii de formule Balmer si inscrie = n1 1; n2 = ∞, obținem:
.
;
.
Primul potențial de excitație U1 au cea mai mică diferență de potențial, care va avea loc în domeniul accelerează de un electron la o coliziune cu un atom de neexcitat-l transfere la prima stare de excitare. Pentru hidrogen, aceasta corespunde unei tranziții de electroni de la prima la a doua orbita Bohr. Asimilarea forța de muncă de accelerare câmp UE1 cuantic electric de energie h # 957;. absorbție atomică în timpul tranziției către prima stare excitată, obținem:
,
.
.
Exemplul 2. O viteză inițială de electroni, care poate fi ignorat a trecut diferența de potențial de accelerare U. Se determină lungimea de undă de Broglie a unui electron în două cazuri: 1) U1 = 51 V; 2) U2 = 510 kV.
mp. mn și mya - respectiv proton în masă, neutroni și nucleu.
Tabelele de căutare în sus sunt date întotdeauna în masă de atomi neutri, dar nici nuclee, deci formula (1) este oportun să se transforme, astfel încât aceasta include masa m un atom neutru. masa atomică neutră egală cu masa nucleului și electronii care constituie învelișul de electroni al atomului: ma = mya + ZME. unde mya = ma - ZME. Apoi, cu formula (1) ia forma:
.
Notând că mp + mi = (masa atomului de hidrogen), în final obținem:
.
Substituind în această expresie valorile numerice ale maselor în uam (A se vedea tabelul 15 și Anexa 17 ..), obținem:
Pentru a calcula formula de utilizare a energiei de legare nucleară
Eb = 931 × 0,04216 MeV = 39.2 MeV.
Exemplul 7. La coliziune # 945; -particles cu miez de bor al reacției nucleare a avut loc, ceea ce a dus la două noi nuclee s-au format. Unul dintre aceste nuclee era atom de hidrogen nucleu. Se determină numărul de secvență și numărul de masă al doilea miez, energia de reacție simbolic nucleară înregistrare și de a determina efectul.
Notăm simbolul nucleu necunoscut. deoarece # 945; -particle este un nucleu de heliu. înregistrarea reacției este:
.
Aplicarea legii de conservare a taxa, obținem ecuația: 2 + 1 = 5 + Z. unde Z = 6. Aplicând legea conservării nucleoni, obținem ecuația: 4 + 10 = 1 + A. unde A = 13. De aceea, miezul necunoscut este nucleul atomului izotopului de carbon. Acum putem scrie reacția nucleară în forma sa finală:
.
Q efect energetic al reacției nucleare se determină prin formula:
Înlocuirea masei inițiale a produșilor de reacție nucleii și nuclee de greutate ale maselor de atomi neutri (. Tabelul 15 a se vedea apendicele) și substituirea acestora în formula de calcul, obținem:
Q = 931 [4.00260 + 10.01294) - (+ 13.00335 1.00783)] = MeV 4,06 MeV.
Răspuns: Q = 4,06 MeV.
Exemplul 8. Identificarea energiei de reacție de 10 V (n, # 945;) 7 Li. care curge din interacțiunea neutronilor cu nuclee de repaus bor foarte lent. Găsiți, de asemenea, energia cinetică a produșilor de reacție.
În reacția nucleară 10 (n, # 945;) 7 Li este după cum urmează. miez de bor. absorbind un neutron lent. transformat într-un miez intermediar. Acestea din urmă, fiind excitat, emite # 945; -particle (adică heliu nucleu), transformându-se în miez de litiu. In forma extinsă a reacției este scris după cum urmează:
.
Energia de reacție nucleară (sau căldura de reacție) Q este determinată prin formula:
Înlocuirea masa de repaus a nucleelor atomice ale atomilor se odihnesc masele (.., A se vedea Tabelul 15, Anexa) obținem:
- 4.00260) = MeV 2.8 MeV.
Pentru a găsi energia cinetică a produșilor de reacție - litiu 7 nuclee și Li # 945; -particles, se aplică legea de conservare a dreptului relativistă de conservare a energiei și a impulsului:
;
luând în considerare ecuația (1) obținem:
Dintre condițiile problemei, rezultă că valorile TB și pot fi neglijate Tn. Apoi vom ajunge la suma energiilor cinetice ale particulelor 7 Li și 4 El:
Conform legii conservării impulsului :.
Presupunând că impulsul total al particulelor la reacția să fie zero, obținem:
.
Prin urmare, pentru modulele de impulsuri au :.
Particulele leguminoaselor și energia lor cinetică sunt legate. Prin urmare:
Rezolvarea sistemului de ecuații (2) și (3):
.
.
.
Exemplul 9. pozitroni cu energia cinetică T = 0,75 incidente MeV pe repaus electron liber. Ca urmare, există două anihilare # 947; foton cu aceeași energie. Se determină unghiul # 952; între direcțiile de expansiune.
T = 0,75 MeV = 0,75 x 1,6 x 10 -13 J m0 = 9,1 x 10 -31 kg e1 = e2 = e
Procesul de anihilare a electronilor e - și e + pozitron are loc schema e - + e + → # 947 + # 947; și se supune
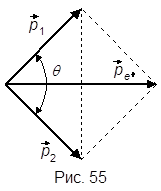
În același timp. unde # 949; - energia fiecărui # 947; -photon.
Din figura 55 obținem. atunci:
(*)
Pentru a calcula unghiul # 952;. este necesar să se determine forța și energia pozitroni # 949; fiecare # 947; -photon. pozitroni Impulse găsi știind T. sale energia cinetică Deoarece valoarea T depășește energia de repaus a pozitroni m0c 2 = 0,511 MeV, pozitroni ar trebui să fie considerată ca o particulă relativistă. În acest caz, impulsul particulei este exprimată prin formula.
energie # 947; -photon # 949; determinată folosind legea de conservare a energiei relativiste:
,
în cazul în care - suma energiilor particulelor la restul reacției, și - suma energiilor cinetice. În dreapta sunt cantitățile aferente particulelor după reacție. Având în vedere faptul că masa de repaus a fotonului este zero :. și energia totală a fotonilor au energia cinetică, adică, . și de electroni și pozitroni au același rest M0 în masă. Obținem.
Substituind în ecuația (*), # 2 valoarea 949, iar valoarea pulsului pozitroni. găsi:
.
Deoarece energia restului de electroni (pozitroni) m0c 2 = 0,511 MeV, obținem:
; .