Generale și eșantion de populație - studopediya

Statistică matematică - o știință care, pe baza metodelor de teoria probabilităților, este angajată în sistematizarea și prelucrarea datelor statistice pentru concluzii științifice și practice.

Datele statistice menționate la datele privind numărul de obiecte cu aceste sau alte atribute.

obiecte pentru grupuri unite printr-o trăsătură calitativă sau cantitativă, numită populația statistică. Obiectele incluse în total, sunt numite elementele sale, iar numărul total al acestora - volumul său.

Populația generală este un set de toate observațiile posibile posibile care ar putea fi făcute la un anumit condiții reale sau complexe mai îndeaproape: populația este numită x variabilă aleatoare și spațiul de probabilitate asociat.

Distribuția variabila aleatoare X se numește distribuția populației (să zicem, de exemplu, o distribuție normală sau o populație generală normală).

De exemplu, dacă numărul de măsurători independente realizate din variabila x aleatoare, populația generală este teoretic infinită (adică populația generală - abstract condiționat - conceptul matematic); în cazul în care a verificat numărul de elemente defecte în lotul de N elemente, atunci acest joc este considerat ca volumul final al populației generale N.

În cazul în care numărul de obiecte N este suficient de mare, este dificil să se efectueze un recensământ, și uneori imposibil fizic (de exemplu, pentru a verifica calitatea tuturor runde). Apoi, selectate aleatoriu din întregul număr limitat populație de obiecte și supuse la studiul lor.

Proba globală sau un eșantion de mărime n este x1 secvență. x2. ..., xn de variabile aleatoare identic distribuite independent, distribuția fiecăreia dintre care coincide cu distribuția variabilei x aleatoare.

De exemplu, n primele masuratori variabila aleatoare X este de obicei considerată ca un eșantion de volum infinit n în populație. Datele obținute se numește observație aleatoare x variabilă, și este, de asemenea, a spus că variabila aleatoare X „ia valoarea“ x1. x2. ..., xn.

Sarcina principală a statisticii matematice - pentru a face concluzii bazate pe dovezi cu privire la distribuirea unuia sau mai multor necunoscute variabile aleatoare și relația lor unul cu altul. Metoda constă în faptul că, în funcție de proprietățile și caracteristicile eșantionului pentru a trage concluzii cu privire la caracteristicile și valorile numerice ale unei legi de distribuție aleatorie (populație) se numește o metodă de eșantionare.

Pentru caracteristici de valoare aleatoare obținute prin metoda de eșantionare, au fost obiectiv, este necesar ca eșantionul a fost reprezentativ, adică destul de bine reprezentat valoarea investigate. Legea numerelor mari poate argumenta că eșantionul este reprezentativ, în cazul în care se efectuează în mod aleatoriu, și anume toate obiectele din totalul populației au aceeași probabilitate de a fi incluși în eșantion. Există diferite tipuri de selecție a eșantionului.

1. O selecție aleatoare simplă se numește o selecție, în care obiectele sunt preluate unul câte unul din întreaga populație.

2. stratificata (stratificat) de selecție constă în faptul că volumul set general inițial este subdivizat în subseturi N (straturi) N1. N2, ..., Nk. astfel încât N1 + N2 + ... + Nk = N. Când striatii determinată din fiecare dintre aceste extras eșantion simplu aleator de dimensiune n1. n2. ..., nk. Un caz special de eșantionare stratificată este o selecție tipică, în care obiectele selectate nu sunt din întreaga populație, și fiecare parte tipic.

Selecția combinată combină mai multe tipuri de selecție, formând diferite sondaj de fază. Există și alte metode de proiectare probă.

Proba se numește din nou, în cazul în care obiectul selectat la alegerea următoare a revenit la populația generală. Proba se numește citire-o dată, în cazul în care obiectul selectat în populația generală nu este rambursabil. Pentru final populația generală eșantionarea aleatorie fără înlocuire la fiecare pas conduce la o dependență a observațiilor individuale, selecție aleatorie la fel de probabil să se întoarcă - observațiile sunt independente. În practică, de obicei, face cu probe-repetiție liberă. Cu toate acestea, atunci când mărimea populației N este de multe ori mai mare decât mărimea eșantionului n (de exemplu, sute sau mii de ori), dependența de observare poate fi neglijată.

Astfel, un eșantion aleatoriu x1. x2. ..., xn - este rezultatul unor observații succesive și independente ale ξ variabile aleatoare, reprezentând populația generală, și toate elementele au aceeași distribuție de eșantionare că originalul aleatoare x variabila.

Fx Funcția de distribuție (x), și alte caracteristici numerice ale variabilei x aleatoare va fi numit teoretic, spre deosebire de caracteristicile de probă. care sunt determinate pe baza rezultatelor observațiilor.

Lăsați proba x1. x2. ..., xk este rezultatul unor observații independente ale variabilei x aleatoare, și x1 observate ori x2 - n1 ori n2, ..., xk - NK ori, astfel încât ni = n - mărimea eșantionului. Numărul Ni. care indică de câte ori xi valoarea apărut în n observații se numește frecvența valorilor și Ni raportul / n = Wi - frecvența relativă. Este evident că numărul de wi și rațional.

Populația statistică, situată în ordinea crescătoare a caracteristică, numită seria variațional. Membrii săi reprezintă x (1). x (2), ... x (n) și numitele variante de realizare. Numărul de variație se numește discret. în cazul în care membrii săi să ia valori izolate din beton. Eșantionarea statistică distribuția unei variabile x aleatoare discreta se spune lista de opțiuni și Wi frecvența relativă corespunzătoare. Tabelul rezultat se numește seria statistică.

Fig. 7.1.3 și 7.1.4, construite în conformitate cu tabelul 7.1.2, histograma prezentată și graficul de frecvență cumulativă. Curbele corespund densității funcției de distribuție normală, „potrivire“ a datelor.

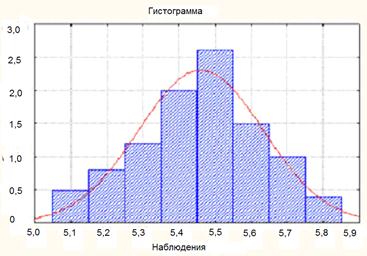
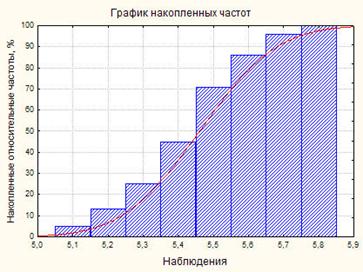
Astfel, distribuția eșantionului este o distribuție aproximare a populației.