Ce este punctele staționare și critice cum să le găsească

În primul rând, vom scrie ecuația unei funcții matematice

unde x - argumentul funcției, și în - funcția în sine. Adică, am stabilit nici o valoare a argumentului x, și se calculează prin ecuația (1), valoarea funcției în acel punct. Accepted trage graficul y = f (x). Desen axele coordonate x și y. Valoarea lui x este reprezentată grafic de-a lungul axei orizontale x. Această axă se numește axa x. Vertical amâna valoarea calculată a funcției y (această axă se numește axa verticală). Cifra este un grafic al unei funcții

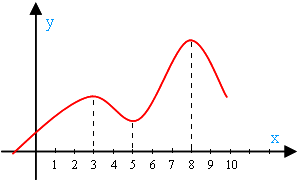
După cum putem vedea la x = 3 și x = 8 funcție maximă. Și când x = 5, funcția are un minim. Aceasta este, funcția y = f (x) poate avea atat minima si maxima. așa

Punctul maxim - valoarea lui x pentru care funcția are un maxim.

punctul minim - valoarea lui x pentru care funcția are o valoare minimă.

Ambele aceste puncte sunt numite cuvântul comun - extremă. Aceasta este, la punctele de extremelor funcției are o valoare maximă sau minimă.

Mai avem nevoie să cunoaștem ce derivata funcției. Dacă știm funcția în sine (1), atunci derivatul este luată după cum urmează:

Sensul unui derivat - panta funcției în punctul x. Ea poate fi efectuată în orice punct al liniei funcției tangentă și unghiul dintre această tangentă și axa x va determina unghiul de înclinare. Dar este mai convenabil să se calculeze nu unghiul de înclinare a, și tangenta unghiului tg. Cu alte cuvinte,

tgα = dy / dx = df (x) / dx (3)

După cum se vede din figura de mai sus la punctele tgα funcția extremum = 0. Aceasta este, derivata de la aceste puncte este egal cu zero. Dacă cunoaștem funcția ecuației (1), setarea derivatului la zero, obținem ecuația algebrică pentru calcularea punctelor maxime și minime

Și ceea ce este punctele critice și staționare ale funcției? Funcția punctul extremum (adică, în cazul în care funcția are o valoare maximă sau minimă), uneori, de asemenea, numite puncte fixe. Aceasta este figura de mai sus punctul x = 3, 5 și 8. Se întâmplă uneori că funcția y (x) are capete, care este, funcția curba nu merge la infinit sau spre stânga sau spre dreapta. De exemplu, în figura de mai sus, se va presupune că această caracteristică este situată între punctele x = -1 și x = 10. Dacă, în punctele extreme ale acestor funcții ar avea un minim (sau maxim), adică extremum (derivatul este zero), atunci aceste puncte nu sunt numite staționare.

Dar punctele interne ale funcției în care funcția este continuă, dar în aceste puncte instrumentul derivat nu există, numite puncte critice. A se vedea figura de mai jos

La punctul x = 0, această funcție are un maxim, dar în acest moment există o fractură și funcții. Un vârf ascuțit. Derivatul (panta funcției) la stânga de la punctul x = 0 este pozitiv, și la dreapta acestui punct derivatul este negativ. Acesta este un punct critic. Dar, la punctul x = 1 există un minim (derivata este zero), dar funcția își schimbă semnul fără fractură (adică, treptat). Acesta este punctul minim și punct fix.